26 Numerics library [numerics]
26.1 General [numerics.general]
This Clause describes components that C++ programs may use to perform seminumerical operations.
The following subclauses describe components for complex number types, random number generation, numeric (n-at-a-time) arrays, generalized numeric algorithms, and facilities included from the ISO C library, as summarized in Table [tab:numerics.lib.summary].
| Subclause | Header(s) | |
| [numeric.requirements] | Requirements | |
| [cfenv] | Floating-Point Environment | <cfenv> |
| [complex.numbers] | Complex Numbers | <complex> |
| [rand] | Random number generation | <random> |
| [numarray] | Numeric arrays | <valarray> |
| [numeric.ops] | Generalized numeric operations | <numeric> |
| [c.math] | C library | <cmath> |
| <ctgmath> | ||
| <tgmath.h> | ||
| <cstdlib> | ||
26.2 Numeric type requirements [numeric.requirements]
The complex and valarray components are parameterized by the type of information they contain and manipulate. A C++ program shall instantiate these components only with a type T that satisfies the following requirements:273
T is not an abstract class (it has no pure virtual member functions);
T is not a reference type;
T is not cv-qualified;
If T is a class, it has a public default constructor;
If T is a class, it has a public copy constructor with the signature T::T(const T&)
If T is a class, it has a public destructor;
If T is a class, it has a public assignment operator whose signature is either T& T::operator=(const T&) or T& T::operator=(T)
If T is a class, its assignment operator, copy and default constructors, and destructor shall correspond to each other in the following sense: Initialization of raw storage using the default constructor, followed by assignment, is semantically equivalent to initialization of raw storage using the copy constructor. Destruction of an object, followed by initialization of its raw storage using the copy constructor, is semantically equivalent to assignment to the original object.
[ Note: This rule states that there shall not be any subtle differences in the semantics of initialization versus assignment. This gives an implementation considerable flexibility in how arrays are initialized.
[ Example: An implementation is allowed to initialize a valarray by allocating storage using the new operator (which implies a call to the default constructor for each element) and then assigning each element its value. Or the implementation can allocate raw storage and use the copy constructor to initialize each element. — end example ]
If the distinction between initialization and assignment is important for a class, or if it fails to satisfy any of the other conditions listed above, the programmer should use vector ([vector]) instead of valarray for that class; — end note ]
If T is a class, it does not overload unary operator&.
If any operation on T throws an exception the effects are undefined.
In addition, many member and related functions of valarray<T> can be successfully instantiated and will exhibit well-defined behavior if and only if T satisfies additional requirements specified for each such member or related function.
[ Example: It is valid to instantiate valarray<complex>, but operator>() will not be successfully instantiated for valarray<complex> operands, since complex does not have any ordering operators. — end example ]
In other words, value types. These include arithmetic types, pointers, the library class complex, and instantiations of valarray for value types.
26.3 The floating-point environment [cfenv]
26.3.1 Header <cfenv> synopsis [cfenv.syn]
namespace std {
// types
typedef object type fenv_t;
typedef integer type fexcept_t;
// functions
int feclearexcept(int except);
int fegetexceptflag(fexcept_t* pflag, int except);
int feraiseexcept(int except);
int fesetexceptflag(const fexcept_t* pflag, int except);
int fetestexcept(int except);
int fegetround(void);
int fesetround(int mode);
int fegetenv(fenv_t* penv);
int feholdexcept(fenv_t* penv);
int fesetenv(const fenv_t* penv);
int feupdateenv(const fenv_t* penv);
}
The header also defines the macros:
FE_ALL_EXCEPT FE_DIVBYZERO FE_INEXACT FE_INVALID FE_OVERFLOW FE_UNDERFLOW FE_DOWNWARD FE_TONEAREST FE_TOWARDZERO FE_UPWARD FE_DFL_ENV
The header defines all functions, types, and macros the same as Clause 7.6 of the C standard.
The floating-point environment has thread storage duration ([basic.stc.thread]). The initial state for a thread's floating-point environment is the state of the floating-point environment of the thread that constructs the corresponding std::thread object ([thread.thread.class]) at the time it constructed the object. [ Note: That is, the child thread gets the floating-point state of the parent thread at the time of the child's creation. — end note ]
A separate floating-point environment shall be maintained for each thread. Each function accesses the environment corresponding to its calling thread.
26.4 Complex numbers [complex.numbers]
The header <complex> defines a class template, and numerous functions for representing and manipulating complex numbers.
The effect of instantiating the template complex for any type other than float, double, or long double is unspecified. The specializations complex<float>, complex<double>, and complex<long double> are literal types ([basic.types]).
If the result of a function is not mathematically defined or not in the range of representable values for its type, the behavior is undefined.
If z is an lvalue expression of type cv std::complex<T> then:
the expression reinterpret_cast<cv T(&)[2]>(z) shall be well-formed,
reinterpret_cast<cv T(&)[2]>(z)[0] shall designate the real part of z, and
reinterpret_cast<cv T(&)[2]>(z)[1] shall designate the imaginary part of z.
Moreover, if a is an expression of type cv std::complex<T>* and the expression a[i] is well-defined for an integer expression i, then:
reinterpret_cast<cv T*>(a)[2*i] shall designate the real part of a[i], and
reinterpret_cast<cv T*>(a)[2*i + 1] shall designate the imaginary part of a[i].
26.4.1 Header <complex> synopsis [complex.syn]
namespace std {
template<class T> class complex;
template<> class complex<float>;
template<> class complex<double>;
template<> class complex<long double>;
// [complex.ops], operators:
template<class T>
complex<T> operator+(const complex<T>&, const complex<T>&);
template<class T> complex<T> operator+(const complex<T>&, const T&);
template<class T> complex<T> operator+(const T&, const complex<T>&);
template<class T> complex<T> operator-(
const complex<T>&, const complex<T>&);
template<class T> complex<T> operator-(const complex<T>&, const T&);
template<class T> complex<T> operator-(const T&, const complex<T>&);
template<class T> complex<T> operator*(
const complex<T>&, const complex<T>&);
template<class T> complex<T> operator*(const complex<T>&, const T&);
template<class T> complex<T> operator*(const T&, const complex<T>&);
template<class T> complex<T> operator/(
const complex<T>&, const complex<T>&);
template<class T> complex<T> operator/(const complex<T>&, const T&);
template<class T> complex<T> operator/(const T&, const complex<T>&);
template<class T> complex<T> operator+(const complex<T>&);
template<class T> complex<T> operator-(const complex<T>&);
template<class T> constexpr bool operator==(
const complex<T>&, const complex<T>&);
template<class T> constexpr bool operator==(const complex<T>&, const T&);
template<class T> constexpr bool operator==(const T&, const complex<T>&);
template<class T> constexpr bool operator!=(const complex<T>&, const complex<T>&);
template<class T> constexpr bool operator!=(const complex<T>&, const T&);
template<class T> constexpr bool operator!=(const T&, const complex<T>&);
template<class T, class charT, class traits>
basic_istream<charT, traits>&
operator>>(basic_istream<charT, traits>&, complex<T>&);
template<class T, class charT, class traits>
basic_ostream<charT, traits>&
operator<<(basic_ostream<charT, traits>&, const complex<T>&);
// [complex.value.ops], values:
template<class T> constexpr T real(const complex<T>&);
template<class T> constexpr T imag(const complex<T>&);
template<class T> T abs(const complex<T>&);
template<class T> T arg(const complex<T>&);
template<class T> T norm(const complex<T>&);
template<class T> complex<T> conj(const complex<T>&);
template <class T> complex<T> proj(const complex<T>&);
template<class T> complex<T> polar(const T&, const T& = 0);
// [complex.transcendentals], transcendentals:
template<class T> complex<T> acos(const complex<T>&);
template<class T> complex<T> asin(const complex<T>&);
template<class T> complex<T> atan(const complex<T>&);
template<class T> complex<T> acosh(const complex<T>&);
template<class T> complex<T> asinh(const complex<T>&);
template<class T> complex<T> atanh(const complex<T>&);
template<class T> complex<T> cos (const complex<T>&);
template<class T> complex<T> cosh (const complex<T>&);
template<class T> complex<T> exp (const complex<T>&);
template<class T> complex<T> log (const complex<T>&);
template<class T> complex<T> log10(const complex<T>&);
template<class T> complex<T> pow(const complex<T>&, const T&);
template<class T> complex<T> pow(const complex<T>&, const complex<T>&);
template<class T> complex<T> pow(const T&, const complex<T>&);
template<class T> complex<T> sin (const complex<T>&);
template<class T> complex<T> sinh (const complex<T>&);
template<class T> complex<T> sqrt (const complex<T>&);
template<class T> complex<T> tan (const complex<T>&);
template<class T> complex<T> tanh (const complex<T>&);
// [complex.literals], complex literals:
inline namespace literals {
inline namespace complex_literals {
constexpr complex<long double> operator""il(long double);
constexpr complex<long double> operator""il(unsigned long long);
constexpr complex<double> operator""i(long double);
constexpr complex<double> operator""i(unsigned long long);
constexpr complex<float> operator""if(long double);
constexpr complex<float> operator""if(unsigned long long);
}
}
}
26.4.2 Class template complex [complex]
namespace std {
template<class T>
class complex {
public:
typedef T value_type;
constexpr complex(const T& re = T(), const T& im = T());
constexpr complex(const complex&);
template<class X> constexpr complex(const complex<X>&);
constexpr T real() const;
void real(T);
constexpr T imag() const;
void imag(T);
complex<T>& operator= (const T&);
complex<T>& operator+=(const T&);
complex<T>& operator-=(const T&);
complex<T>& operator*=(const T&);
complex<T>& operator/=(const T&);
complex& operator=(const complex&);
template<class X> complex<T>& operator= (const complex<X>&);
template<class X> complex<T>& operator+=(const complex<X>&);
template<class X> complex<T>& operator-=(const complex<X>&);
template<class X> complex<T>& operator*=(const complex<X>&);
template<class X> complex<T>& operator/=(const complex<X>&);
};
}
The class complex describes an object that can store the Cartesian components, real() and imag(), of a complex number.
26.4.3 complex specializations [complex.special]
namespace std {
template<> class complex<float> {
public:
typedef float value_type;
constexpr complex(float re = 0.0f, float im = 0.0f);
constexpr explicit complex(const complex<double>&);
constexpr explicit complex(const complex<long double>&);
constexpr float real() const;
void real(float);
constexpr float imag() const;
void imag(float);
complex<float>& operator= (float);
complex<float>& operator+=(float);
complex<float>& operator-=(float);
complex<float>& operator*=(float);
complex<float>& operator/=(float);
complex<float>& operator=(const complex<float>&);
template<class X> complex<float>& operator= (const complex<X>&);
template<class X> complex<float>& operator+=(const complex<X>&);
template<class X> complex<float>& operator-=(const complex<X>&);
template<class X> complex<float>& operator*=(const complex<X>&);
template<class X> complex<float>& operator/=(const complex<X>&);
};
template<> class complex<double> {
public:
typedef double value_type;
constexpr complex(double re = 0.0, double im = 0.0);
constexpr complex(const complex<float>&);
constexpr explicit complex(const complex<long double>&);
constexpr double real() const;
void real(double);
constexpr double imag() const;
void imag(double);
complex<double>& operator= (double);
complex<double>& operator+=(double);
complex<double>& operator-=(double);
complex<double>& operator*=(double);
complex<double>& operator/=(double);
complex<double>& operator=(const complex<double>&);
template<class X> complex<double>& operator= (const complex<X>&);
template<class X> complex<double>& operator+=(const complex<X>&);
template<class X> complex<double>& operator-=(const complex<X>&);
template<class X> complex<double>& operator*=(const complex<X>&);
template<class X> complex<double>& operator/=(const complex<X>&);
};
template<> class complex<long double> {
public:
typedef long double value_type;
constexpr complex(long double re = 0.0L, long double im = 0.0L);
constexpr complex(const complex<float>&);
constexpr complex(const complex<double>&);
constexpr long double real() const;
void real(long double);
constexpr long double imag() const;
void imag(long double);
complex<long double>& operator=(const complex<long double>&);
complex<long double>& operator= (long double);
complex<long double>& operator+=(long double);
complex<long double>& operator-=(long double);
complex<long double>& operator*=(long double);
complex<long double>& operator/=(long double);
template<class X> complex<long double>& operator= (const complex<X>&);
template<class X> complex<long double>& operator+=(const complex<X>&);
template<class X> complex<long double>& operator-=(const complex<X>&);
template<class X> complex<long double>& operator*=(const complex<X>&);
template<class X> complex<long double>& operator/=(const complex<X>&);
};
}
26.4.4 complex member functions [complex.members]
template<class T> constexpr complex(const T& re = T(), const T& im = T());
Effects: Constructs an object of class complex.
Postcondition: real() == re && imag() == im.
Returns: The value of the real component.
Effects: Assigns val to the real component.
Returns: The value of the imaginary component.
Effects: Assigns val to the imaginary component.
26.4.5 complex member operators [complex.member.ops]
complex<T>& operator+=(const T& rhs);
Effects: Adds the scalar value rhs to the real part of the complex value *this and stores the result in the real part of *this, leaving the imaginary part unchanged.
Returns: *this.
complex<T>& operator-=(const T& rhs);
Effects: Subtracts the scalar value rhs from the real part of the complex value *this and stores the result in the real part of *this, leaving the imaginary part unchanged.
Returns: *this.
complex<T>& operator*=(const T& rhs);
Effects: Multiplies the scalar value rhs by the complex value *this and stores the result in *this.
Returns: *this.
complex<T>& operator/=(const T& rhs);
Effects: Divides the scalar value rhs into the complex value *this and stores the result in *this.
Returns: *this.
template<class X> complex<T>& operator+=(const complex<X>& rhs);
Effects: Adds the complex value rhs to the complex value *this and stores the sum in *this.
Returns: *this.
template<class X> complex<T>& operator-=(const complex<X>& rhs);
Effects: Subtracts the complex value rhs from the complex value *this and stores the difference in *this.
Returns: *this.
template<class X> complex<T>& operator*=(const complex<X>& rhs);
Effects: Multiplies the complex value rhs by the complex value *this and stores the product in *this.
Returns: *this.
template<class X> complex<T>& operator/=(const complex<X>& rhs);
Effects: Divides the complex value rhs into the complex value *this and stores the quotient in *this.
Returns: *this.
26.4.6 complex non-member operations [complex.ops]
template<class T> complex<T> operator+(const complex<T>& lhs);
Remarks: unary operator.
Returns: complex<T>(lhs).
template<class T> complex<T> operator+(const complex<T>& lhs, const complex<T>& rhs); template<class T> complex<T> operator+(const complex<T>& lhs, const T& rhs); template<class T> complex<T> operator+(const T& lhs, const complex<T>& rhs);
Returns: complex<T>(lhs) += rhs.
template<class T> complex<T> operator-(const complex<T>& lhs);
Remarks: unary operator.
Returns: complex<T>(-lhs.real(),-lhs.imag()).
template<class T>
complex<T> operator-(const complex<T>& lhs, const complex<T>& rhs);
template<class T> complex<T> operator-(const complex<T>& lhs, const T& rhs);
template<class T> complex<T> operator-(const T& lhs, const complex<T>& rhs);
Returns: complex<T>(lhs) -= rhs.
template<class T>
complex<T> operator*(const complex<T>& lhs, const complex<T>& rhs);
template<class T> complex<T> operator*(const complex<T>& lhs, const T& rhs);
template<class T> complex<T> operator*(const T& lhs, const complex<T>& rhs);
Returns: complex<T>(lhs) *= rhs.
template<class T>
complex<T> operator/(const complex<T>& lhs, const complex<T>& rhs);
template<class T> complex<T> operator/(const complex<T>& lhs, const T& rhs);
template<class T> complex<T> operator/(const T& lhs, const complex<T>& rhs);
Returns: complex<T>(lhs) /= rhs.
template<class T>
constexpr bool operator==(const complex<T>& lhs, const complex<T>& rhs);
template<class T> constexpr bool operator==(const complex<T>& lhs, const T& rhs);
template<class T> constexpr bool operator==(const T& lhs, const complex<T>& rhs);
Returns: lhs.real() == rhs.real() && lhs.imag() == rhs.imag().
Remarks: The imaginary part is assumed to be T(), or 0.0, for the T arguments.
template<class T>
constexpr bool operator!=(const complex<T>& lhs, const complex<T>& rhs);
template<class T> constexpr bool operator!=(const complex<T>& lhs, const T& rhs);
template<class T> constexpr bool operator!=(const T& lhs, const complex<T>& rhs);
Returns: rhs.real() != lhs.real() || rhs.imag() != lhs.imag().
template<class T, class charT, class traits>
basic_istream<charT, traits>&
operator>>(basic_istream<charT, traits>& is, complex<T>& x);
Effects: Extracts a complex number x of the form: u, (u), or (u,v), where u is the real part and v is the imaginary part ([istream.formatted]).
Requires: The input values shall be convertible to T.
If bad input is encountered, calls is.setstate(ios_base::failbit) (which may throw ios::failure ([iostate.flags])).
Returns: is.
Remarks: This extraction is performed as a series of simpler extractions. Therefore, the skipping of whitespace is specified to be the same for each of the simpler extractions.
template<class T, class charT, class traits>
basic_ostream<charT, traits>&
operator<<(basic_ostream<charT, traits>& o, const complex<T>& x);
Effects: inserts the complex number x onto the stream o as if it were implemented as follows:
template<class T, class charT, class traits>
basic_ostream<charT, traits>&
operator<<(basic_ostream<charT, traits>& o, const complex<T>& x) {
basic_ostringstream<charT, traits> s;
s.flags(o.flags());
s.imbue(o.getloc());
s.precision(o.precision());
s << '(' << x.real() << "," << x.imag() << ')';
return o << s.str();
}
Note: In a locale in which comma is used as a decimal point character, the use of comma as a field separator can be ambiguous. Inserting std::showpoint into the output stream forces all outputs to show an explicit decimal point character; as a result, all inserted sequences of complex numbers can be extracted unambiguously.
26.4.7 complex value operations [complex.value.ops]
template<class T> constexpr T real(const complex<T>& x);
Returns: x.real().
template<class T> constexpr T imag(const complex<T>& x);
Returns: x.imag().
template<class T> T abs(const complex<T>& x);
Returns: The magnitude of x.
template<class T> T arg(const complex<T>& x);
Returns: The phase angle of x, or atan2(imag(x), real(x)).
template<class T> T norm(const complex<T>& x);
Returns: The squared magnitude of x.
template<class T> complex<T> conj(const complex<T>& x);
Returns: The complex conjugate of x.
template<class T> complex<T> proj(const complex<T>& x);
Returns: The projection of x onto the Riemann sphere.
Remarks: Behaves the same as the C function cproj, defined in 7.3.9.4.
template<class T> complex<T> polar(const T& rho, const T& theta = 0);
Returns: The complex value corresponding to a complex number whose magnitude is rho and whose phase angle is theta.
26.4.8 complex transcendentals [complex.transcendentals]
template<class T> complex<T> acos(const complex<T>& x);
Returns: The complex arc cosine of x.
Remarks: Behaves the same as C function cacos, defined in 7.3.5.1.
template<class T> complex<T> asin(const complex<T>& x);
Returns: The complex arc sine of x.
Remarks: Behaves the same as C function casin, defined in 7.3.5.2.
template<class T> complex<T> atan(const complex<T>& x);
Returns: The complex arc tangent of x.
Remarks: Behaves the same as C function catan, defined in 7.3.5.3.
template<class T> complex<T> acosh(const complex<T>& x);
Returns: The complex arc hyperbolic cosine of x.
Remarks: Behaves the same as C function cacosh, defined in 7.3.6.1.
template<class T> complex<T> asinh(const complex<T>& x);
Returns: The complex arc hyperbolic sine of x.
Remarks: Behaves the same as C function casinh, defined in 7.3.6.2.
template<class T> complex<T> atanh(const complex<T>& x);
Returns: The complex arc hyperbolic tangent of x.
Remarks: Behaves the same as C function catanh, defined in 7.3.6.3.
template<class T> complex<T> cos(const complex<T>& x);
Returns: The complex cosine of x.
template<class T> complex<T> cosh(const complex<T>& x);
Returns: The complex hyperbolic cosine of x.
template<class T> complex<T> exp(const complex<T>& x);
Returns: The complex base e exponential of x.
template<class T> complex<T> log(const complex<T>& x);
Remarks: the branch cuts are along the negative real axis.
Returns: The complex natural (base e) logarithm of x, in the range of a strip mathematically unbounded along the real axis and in the interval [-i times pi,i times pi] along the imaginary axis. When x is a negative real number, imag(log(x)) is pi.
template<class T> complex<T> log10(const complex<T>& x);
Remarks: the branch cuts are along the negative real axis.
Returns: The complex common (base 10) logarithm of x, defined as log(x)/log(10).
template<class T>
complex<T> pow(const complex<T>& x, const complex<T>& y);
template<class T> complex<T> pow (const complex<T>& x, const T& y);
template<class T> complex<T> pow (const T& x, const complex<T>& y);
Remarks: the branch cuts are along the negative real axis.
Returns: The complex power of base x raised to the y-th power, defined as exp(y*log(x)). The value returned for pow(0,0) is implementation-defined.
template<class T> complex<T> sin (const complex<T>& x);
Returns: The complex sine of x.
template<class T> complex<T> sinh (const complex<T>& x);
Returns: The complex hyperbolic sine of x.
template<class T> complex<T> sqrt (const complex<T>& x);
Remarks: the branch cuts are along the negative real axis.
Returns: The complex square root of x, in the range of the right half-plane. If the argument is a negative real number, the value returned lies on the positive imaginary axis.
template<class T> complex<T> tan (const complex<T>& x);
Returns: The complex tangent of x.
template<class T> complex<T> tanh (const complex<T>& x);
Returns: The complex hyperbolic tangent of x.
26.4.9 Additional overloads [cmplx.over]
The additional overloads shall be sufficient to ensure:
If the argument has type long double, then it is effectively cast to complex<long double>.
Otherwise, if the argument has type double or an integer type, then it is effectively cast to complex<double>.
Otherwise, if the argument has type float, then it is effectively cast to complex<float>.
Function template pow shall have additional overloads sufficient to ensure, for a call with at least one argument of type complex<T>:
If either argument has type complex<long double> or type long double, then both arguments are effectively cast to complex<long double>.
Otherwise, if either argument has type complex<double>, double, or an integer type, then both arguments are effectively cast to complex<double>.
Otherwise, if either argument has type complex<float> or float, then both arguments are effectively cast to complex<float>.
26.4.10 Suffixes for complex number literals [complex.literals]
This section describes literal suffixes for constructing complex number literals. The suffixes i, il, and if create complex numbers of the types complex<double>, complex<long double>, and complex<float> respectively, with their imaginary part denoted by the given literal number and the real part being zero.
constexpr complex<long double> operator""il(long double d);
constexpr complex<long double> operator""il(unsigned long long d);
Returns: complex<long double>{0.0L, static_cast<long double>(d)}.
constexpr complex<double> operator""i(long double d);
constexpr complex<double> operator""i(unsigned long long d);
Returns: complex<double>{0.0, static_cast<double>(d)}.
constexpr complex<float> operator""if(long double d);
constexpr complex<float> operator""if(unsigned long long d);
Returns: complex<float>{0.0f, static_cast<float>(d)}.
26.5 Random number generation [rand]
This subclause defines a facility for generating (pseudo-)random numbers.
In addition to a few utilities, four categories of entities are described: uniform random number generators, random number engines, random number engine adaptors, and random number distributions. These categorizations are applicable to types that satisfy the corresponding requirements, to objects instantiated from such types, and to templates producing such types when instantiated. [ Note: These entities are specified in such a way as to permit the binding of any uniform random number generator object e as the argument to any random number distribution object d, thus producing a zero-argument function object such as given by bind(d,e). — end note ]
Each of the entities specified via this subclause has an associated arithmetic type ([basic.fundamental]) identified as result_type. With T as the result_type thus associated with such an entity, that entity is characterized:
as boolean or equivalently as boolean-valued, if T is bool;
otherwise as integral or equivalently as integer-valued, if numeric_limits<T>::is_integer is true;
otherwise as floating or equivalently as real-valued.
If integer-valued, an entity may optionally be further characterized as signed or unsigned, according to numeric_limits<T>::is_signed.
Unless otherwise specified, all descriptions of calculations in this subclause use mathematical real numbers.
Throughout this subclause, the operators bitand , bitor , and xor denote the respective conventional bitwise operations. Further:
the operator rshift denotes a bitwise right shift with zero-valued bits appearing in the high bits of the result, and
the operator lshiftw denotes a bitwise left shift with zero-valued bits appearing in the low bits of the result, and whose result is always taken modulo 2w.
26.5.1 Requirements [rand.req]
26.5.1.1 General requirements [rand.req.genl]
Throughout this subclause [rand], the effect of instantiating a template:
that has a template type parameter named Sseq is undefined unless the corresponding template argument is cv-unqualified and satisfies the requirements of seed sequence ([rand.req.seedseq]).
that has a template type parameter named URNG is undefined unless the corresponding template argument is cv-unqualified and satisfies the requirements of uniform random number generator ([rand.req.urng]).
that has a template type parameter named Engine is undefined unless the corresponding template argument is cv-unqualified and satisfies the requirements of random number engine ([rand.req.eng]).
that has a template type parameter named RealType is undefined unless the corresponding template argument is cv-unqualified and is one of float, double, or long double.
that has a template type parameter named IntType is undefined unless the corresponding template argument is cv-unqualified and is one of short, int, long, long long, unsigned short, unsigned int, unsigned long, or unsigned long long.
that has a template type parameter named UIntType is undefined unless the corresponding template argument is cv-unqualified and is one of unsigned short, unsigned int, unsigned long, or unsigned long long.
Throughout this subclause [rand], phrases of the form “x is an iterator of a specific kind” shall be interpreted as equivalent to the more formal requirement that “x is a value of a type satisfying the requirements of the specified iterator type.”
26.5.1.2 Seed sequence requirements [rand.req.seedseq]
A seed sequence is an object that consumes a sequence of integer-valued data and produces a requested number of unsigned integer values i, 0 ≤ i < 232 , based on the consumed data. [ Note: Such an object provides a mechanism to avoid replication of streams of random variates. This can be useful, for example, in applications requiring large numbers of random number engines. — end note ]
A class S satisfies the requirements of a seed sequence if the expressions shown in Table [tab:SeedSequence] are valid and have the indicated semantics, and if S also satisfies all other requirements of this section [rand.req.seedseq]. In that Table and throughout this section:
T is the type named by S's associated result_type;
q is a value of S and r is a possibly const value of S;
ib and ie are input iterators with an unsigned integer value_type of at least 32 bits;
rb and re are mutable random access iterators with an unsigned integer value_type of at least 32 bits;
ob is an output iterator; and
il is a value of initializer_list<T>.
| Expression | Return type | Pre/post-condition | Complexity |
| S::result_type | T | T is an unsigned integer type ([basic.fundamental]) of at least 32 bits. | compile-time |
| S() | Creates a seed sequence with the same initial state as all other default-constructed seed sequences of type S. | constant | |
| S(ib,ie) | Creates a seed sequence having internal state that depends on some or all of the bits of the supplied sequence [ib,ie). | Ο(ie - ib) | |
| S(il) | Same as S(il.begin(), il.end()). | same as S(il.begin(), il.end()) | |
| q.generate(rb,re) | void | Does nothing if rb == re. Otherwise, fills the supplied sequence [rb,re) with 32-bit quantities that depend on the sequence supplied to the constructor and possibly also depend on the history of generate's previous invocations. | Ο(re - rb) |
| r.size() | size_t | The number of 32-bit units that would be copied by a call to r.param. | constant |
| r.param(ob) | void | Copies to the given destination a sequence of 32-bit units that can be provided to the constructor of a second object of type S, and that would reproduce in that second object a state indistinguishable from the state of the first object. | Ο(r.size()) |
26.5.1.3 Uniform random number generator requirements [rand.req.urng]
A uniform random number generator g of type G is a function object returning unsigned integer values such that each value in the range of possible results has (ideally) equal probability of being returned. [ Note: The degree to which g's results approximate the ideal is often determined statistically. — end note ]
A class G satisfies the requirements of a uniform random number generator if the expressions shown in Table [tab:UniformRandomNumberGenerator] are valid and have the indicated semantics, and if G also satisfies all other requirements of this section [rand.req.urng]. In that Table and throughout this section:
T is the type named by G's associated result_type, and
g is a value of G.
| Expression | Return type | Pre/post-condition | Complexity |
| G::result_type | T | T is an unsigned integer type ([basic.fundamental]). | compile-time |
| g() | T | Returns a value in the closed interval [G::min(), G::max()]. | amortized constant |
| G::min() | T | Denotes the least value potentially returned by operator(). | compile-time |
| G::max() | T | Denotes the greatest value potentially returned by operator(). | compile-time |
26.5.1.4 Random number engine requirements [rand.req.eng]
A random number engine (commonly shortened to engine) e of type E is a uniform random number generator that additionally meets the requirements (e.g., for seeding and for input/output) specified in this section.
At any given time, e has a state ei for some integer i ≥ 0. Upon construction, e has an initial state e0. An engine's state may be established via a constructor, a seed function, assignment, or a suitable operator>>.
E's specification shall define:
the size of E's state in multiples of the size of result_type, given as an integral constant expression;
the transition algorithm TA by which e's state ei is advanced to its successor state ei+1; and
the generation algorithm GA by which an engine's state is mapped to a value of type result_type.
A class E that satisfies the requirements of a uniform random number generator ([rand.req.urng]) also satisfies the requirements of a random number engine if the expressions shown in Table [tab:RandomEngine] are valid and have the indicated semantics, and if E also satisfies all other requirements of this section [rand.req.eng]. In that Table and throughout this section:
T is the type named by E's associated result_type;
e is a value of E, v is an lvalue of E, x and y are (possibly const) values of E;
s is a value of T;
q is an lvalue satisfying the requirements of a seed sequence ([rand.req.seedseq]);
z is a value of type unsigned long long;
os is an lvalue of the type of some class template specialization basic_ostream<charT, traits>; and
is is an lvalue of the type of some class template specialization basic_istream<charT, traits>;
where charT and traits are constrained according to Clause [strings] and Clause [input.output].
| Expression | Return type | Pre/post-condition | Complexity |
| E() | Creates an engine with the same initial state as all other default-constructed engines of type E. | Ο(size of state) | |
| E(x) | Creates an engine that compares equal to x. | Ο(size of state) | |
| E(s) | Creates an engine with initial state determined by s. | Ο(size of state) | |
| E(q)274 | Creates an engine with an initial state that depends on a sequence produced by one call to q.generate. | same as complexity of q.generate called on a sequence whose length is size of state | |
| e.seed() | void | post: e == E(). | same as E() |
| e.seed(s) | void | post: e == E(s). | same as E(s) |
| e.seed(q) | void | post: e == E(q). | same as E(q) |
| e() | T | Advances e's state ei to ei+1 = TA(ei) and returns GA(ei). | per Table [tab:UniformRandomNumberGenerator] |
| e.discard(z) 275 | void | Advances e's state ei to ei+z by any means equivalent to z consecutive calls e(). | no worse than the complexity of z consecutive calls e() |
| x == y | bool | This operator is an equivalence relation. With Sx and Sy as the infinite sequences of values that would be generated by repeated future calls to x() and y(), respectively, returns true if Sx = Sy ; else returns false. | Ο(size of state) |
| x != y | bool | !(x == y). | Ο(size of state) |
| os << x | reference to the type of os | With os.fmtflags set to ios_base::dec|ios_base::left and the fill character set to the space character, writes to os the textual representation of x's current state. In the output, adjacent numbers are separated by one or more space characters. post: The os.fmtflags and fill character are unchanged. | Ο(size of state) |
| is >> v | reference to the type of is | With is.fmtflags set to ios_base::dec, sets v's state as determined by reading its textual representation from is. If bad input is encountered, ensures that v's state is unchanged by the operation and calls is.setstate(ios::failbit) (which may throw ios::failure [[iostate.flags]]). If a textual representation written via os << x was subsequently read via is >> v, then x == v provided that there have been no intervening invocations of x or of v. pre: is provides a textual representation that was previously written using an output stream whose imbued locale was the same as that of is, and whose type's template specialization arguments charT and traits were respectively the same as those of is. post: The is.fmtflags are unchanged. | Ο(size of state) |
E shall meet the requirements of CopyConstructible (Table [copyconstructible]) and CopyAssignable (Table [copyassignable]) types. These operations shall each be of complexity no worse than Ο(size of state).
This constructor (as well as the subsequent corresponding seed() function) may be particularly useful to applications requiring a large number of independent random sequences.
This operation is common in user code, and can often be implemented in an engine-specific manner so as to provide significant performance improvements over an equivalent naive loop that makes z consecutive calls e().
26.5.1.5 Random number engine adaptor requirements [rand.req.adapt]
A random number engine adaptor (commonly shortened to adaptor) a of type A is a random number engine that takes values produced by some other random number engine, and applies an algorithm to those values in order to deliver a sequence of values with different randomness properties. An engine b of type B adapted in this way is termed a base engine in this context. The expression a.base() shall be valid and shall return a const reference to a's base engine.
The requirements of a random number engine type shall be interpreted as follows with respect to a random number engine adaptor type.
A::A();
Effects: The base engine is initialized as if by its default constructor.
bool operator==(const A& a1, const A& a2);
Returns: true if a1's base engine is equal to a2's base engine. Otherwise returns false.
A::A(result_type s);
Effects: The base engine is initialized with s.
template<class Sseq> void A::A(Sseq& q);
Effects: The base engine is initialized with q.
void seed();
Effects: With b as the base engine, invokes b.seed().
void seed(result_type s);
Effects: With b as the base engine, invokes b.seed(s).
template<class Sseq> void seed(Sseq& q);
Effects: With b as the base engine, invokes b.seed(q).
A shall also satisfy the following additional requirements:
The complexity of each function shall not exceed the complexity of the corresponding function applied to the base engine.
The state of A shall include the state of its base engine. The size of A's state shall be no less than the size of the base engine.
Copying A's state (e.g., during copy construction or copy assignment) shall include copying the state of the base engine of A.
The textual representation of A shall include the textual representation of its base engine.
26.5.1.6 Random number distribution requirements [rand.req.dist]
A random number distribution (commonly shortened to distribution) d of type D is a function object returning values that are distributed according to an associated mathematical probability density function p(z) or according to an associated discrete probability function P(zi). A distribution's specification identifies its associated probability function p(z) or P(zi).
An associated probability function is typically expressed using certain externally-supplied quantities known as the parameters of the distribution. Such distribution parameters are identified in this context by writing, for example, p(z | a,b) or P(zi | a,b), to name specific parameters, or by writing, for example, p(z |{p}) or P(zi |{p}), to denote a distribution's parameters p taken as a whole.
A class D satisfies the requirements of a random number distribution if the expressions shown in Table [tab:RandomDistribution] are valid and have the indicated semantics, and if D and its associated types also satisfy all other requirements of this section [rand.req.dist]. In that Table and throughout this section,
T is the type named by D's associated result_type;
P is the type named by D's associated param_type;
d is a value of D, and x and y are (possibly const) values of D;
glb and lub are values of T respectively corresponding to the greatest lower bound and the least upper bound on the values potentially returned by d's operator(), as determined by the current values of d's parameters;
p is a (possibly const) value of P;
g, g1, and g2 are lvalues of a type satisfying the requirements of a uniform random number generator [[rand.req.urng]];
os is an lvalue of the type of some class template specialization basic_ostream<charT, traits>; and
is is an lvalue of the type of some class template specialization basic_istream<charT, traits>;
where charT and traits are constrained according to Clauses [strings] and [input.output].
| Expression | Return type | Pre/post-condition | Complexity |
| D::result_type | T | T is an arithmetic type ([basic.fundamental]). | compile-time |
| D::param_type | P | compile-time | |
| D() | Creates a distribution whose behavior is indistinguishable from that of any other newly default-constructed distribution of type D. | constant | |
| D(p) | Creates a distribution whose behavior is indistinguishable from that of a distribution newly constructed directly from the values used to construct p. | same as p's construction | |
| d.reset() | void | Subsequent uses of d do not depend on values produced by any engine prior to invoking reset. | constant |
| x.param() | P | Returns a value p such that D(p).param() == p. | no worse than the complexity of D(p) |
| d.param(p) | void | post: d.param() == p. | no worse than the complexity of D(p) |
| d(g) | T | With p = d.param(), the sequence of numbers returned by successive invocations with the same object g is randomly distributed according to the associated p(z |{p}) or P(zi |{p}) function. | amortized constant number of invocations of g |
| d(g,p) | T | The sequence of numbers returned by successive invocations with the same objects g and p is randomly distributed according to the associated p(z |{p}) or P(zi |{p}) function. | amortized constant number of invocations of g |
| x.min() | T | Returns glb. | constant |
| x.max() | T | Returns lub. | constant |
| x == y | bool | This operator is an equivalence relation. Returns true if x.param() == y.param() and S1 = S2 , where S1 and S2 are the infinite sequences of values that would be generated, respectively, by repeated future calls to x(g1) and y(g2) whenever g1 == g2. Otherwise returns false. | constant |
| x != y | bool | !(x == y). | same as x == y. |
| os << x | reference to the type of os | Writes to os a textual representation for the parameters and the additional internal data of x. post: The os.fmtflags and fill character are unchanged. | |
| is >> d | reference to the type of is | Restores from is the parameters and additional internal data of the lvalue d. If bad input is encountered, ensures that d is unchanged by the operation and calls is.setstate(ios::failbit) (which may throw ios::failure [[iostate.flags]]). pre: is provides a textual representation that was previously written using an os whose imbued locale and whose type's template specialization arguments charT and traits were the same as those of is. post: The is.fmtflags are unchanged. |
D shall satisfy the requirements of CopyConstructible (Table [copyconstructible]) and CopyAssignable (Table [copyassignable]) types.
The sequence of numbers produced by repeated invocations of d(g) shall be independent of any invocation of os << d or of any const member function of D between any of the invocations d(g).
If a textual representation is written using os << x and that representation is restored into the same or a different object y of the same type using is >> y, repeated invocations of y(g) shall produce the same sequence of numbers as would repeated invocations of x(g).
It is unspecified whether D::param_type is declared as a (nested) class or via a typedef. In this subclause [rand], declarations of D::param_type are in the form of typedefs for convenience of exposition only.
P shall satisfy the requirements of CopyConstructible (Table [copyconstructible]), CopyAssignable (Table [copyassignable]), and EqualityComparable (Table [equalitycomparable]) types.
For each of the constructors of D taking arguments corresponding to parameters of the distribution, P shall have a corresponding constructor subject to the same requirements and taking arguments identical in number, type, and default values. Moreover, for each of the member functions of D that return values corresponding to parameters of the distribution, P shall have a corresponding member function with the identical name, type, and semantics.
26.5.2 Header <random> synopsis [rand.synopsis]
#include <initializer_list>
namespace std {
// [rand.eng.lcong], class template linear_congruential_engine
template<class UIntType, UIntType a, UIntType c, UIntType m>
class linear_congruential_engine;
// [rand.eng.mers], class template mersenne_twister_engine
template<class UIntType, size_t w, size_t n, size_t m, size_t r,
UIntType a, size_t u, UIntType d, size_t s,
UIntType b, size_t t,
UIntType c, size_t l, UIntType f>
class mersenne_twister_engine;
// [rand.eng.sub], class template subtract_with_carry_engine
template<class UIntType, size_t w, size_t s, size_t r>
class subtract_with_carry_engine;
// [rand.adapt.disc], class template discard_block_engine
template<class Engine, size_t p, size_t r>
class discard_block_engine;
// [rand.adapt.ibits], class template independent_bits_engine
template<class Engine, size_t w, class UIntType>
class independent_bits_engine;
// [rand.adapt.shuf], class template shuffle_order_engine
template<class Engine, size_t k>
class shuffle_order_engine;
// [rand.predef], engines and engine adaptors with predefined parameters
typedef see below minstd_rand0;
typedef see below minstd_rand;
typedef see below mt19937;
typedef see below mt19937_64;
typedef see below ranlux24_base;
typedef see below ranlux48_base;
typedef see below ranlux24;
typedef see below ranlux48;
typedef see below knuth_b;
typedef see below default_random_engine;
// [rand.device], class random_device
class random_device;
// [rand.util.seedseq], class seed_seq
class seed_seq;
// [rand.util.canonical], function template generate_canonical
template<class RealType, size_t bits, class URNG>
RealType generate_canonical(URNG& g);
// [rand.dist.uni.int], class template uniform_int_distribution
template<class IntType = int>
class uniform_int_distribution;
// [rand.dist.uni.real], class template uniform_real_distribution
template<class RealType = double>
class uniform_real_distribution;
// [rand.dist.bern.bernoulli], class bernoulli_distribution
class bernoulli_distribution;
// [rand.dist.bern.bin], class template binomial_distribution
template<class IntType = int>
class binomial_distribution;
// [rand.dist.bern.geo], class template geometric_distribution
template<class IntType = int>
class geometric_distribution;
// [rand.dist.bern.negbin], class template negative_binomial_distribution
template<class IntType = int>
class negative_binomial_distribution;
// [rand.dist.pois.poisson], class template poisson_distribution
template<class IntType = int>
class poisson_distribution;
// [rand.dist.pois.exp], class template exponential_distribution
template<class RealType = double>
class exponential_distribution;
// [rand.dist.pois.gamma], class template gamma_distribution
template<class RealType = double>
class gamma_distribution;
// [rand.dist.pois.weibull], class template weibull_distribution
template<class RealType = double>
class weibull_distribution;
// [rand.dist.pois.extreme], class template extreme_value_distribution
template<class RealType = double>
class extreme_value_distribution;
// [rand.dist.norm.normal], class template normal_distribution
template<class RealType = double>
class normal_distribution;
// [rand.dist.norm.lognormal], class template lognormal_distribution
template<class RealType = double>
class lognormal_distribution;
// [rand.dist.norm.chisq], class template chi_squared_distribution
template<class RealType = double>
class chi_squared_distribution;
// [rand.dist.norm.cauchy], class template cauchy_distribution
template<class RealType = double>
class cauchy_distribution;
// [rand.dist.norm.f], class template fisher_f_distribution
template<class RealType = double>
class fisher_f_distribution;
// [rand.dist.norm.t], class template student_t_distribution
template<class RealType = double>
class student_t_distribution;
// [rand.dist.samp.discrete], class template discrete_distribution
template<class IntType = int>
class discrete_distribution;
// [rand.dist.samp.pconst], class template piecewise_constant_distribution
template<class RealType = double>
class piecewise_constant_distribution;
// [rand.dist.samp.plinear], class template piecewise_linear_distribution
template<class RealType = double>
class piecewise_linear_distribution;
} // namespace std
26.5.3 Random number engine class templates [rand.eng]
Each type instantiated from a class template specified in this section [rand.eng] satisfies the requirements of a random number engine ([rand.req.eng]) type.
Except where specified otherwise, the complexity of each function specified in this section [rand.eng] is constant.
Except where specified otherwise, no function described in this section [rand.eng] throws an exception.
Descriptions are provided in this section [rand.eng] only for engine operations that are not described in [rand.req.eng] or for operations where there is additional semantic information. In particular, declarations for copy constructors, for copy assignment operators, for streaming operators, and for equality and inequality operators are not shown in the synopses.
Each template specified in this section [rand.eng] requires one or more relationships, involving the value(s) of its non-type template parameter(s), to hold. A program instantiating any of these templates is ill-formed if any such required relationship fails to hold.
For every random number engine and for every random number engine adaptor X defined in this sub-clause ([rand.eng]) and in sub-clause [rand.adapt]:
if the constructor
template <class Sseq> explicit X(Sseq& q);
is called with a type Sseq that does not qualify as a seed sequence, then this constructor shall not participate in overload resolution;
if the member function
template <class Sseq> void seed(Sseq& q);
is called with a type Sseq that does not qualify as a seed sequence, then this function shall not participate in overload resolution.
The extent to which an implementation determines that a type cannot be a seed sequence is unspecified, except that as a minimum a type shall not qualify as a seed sequence if it is implicitly convertible to X::result_type.
26.5.3.1 Class template linear_congruential_engine [rand.eng.lcong]
A linear_congruential_engine random number engine produces unsigned integer random numbers. The state xi of a linear_congruential_engine object x is of size 1 and consists of a single integer. The transition algorithm is a modular linear function of the form TA(xi) = (a · xi + c) mod m; the generation algorithm is GA(xi) = xi+1 .
template<class UIntType, UIntType a, UIntType c, UIntType m>
class linear_congruential_engine{
public:
// types
typedef UIntType result_type;
// engine characteristics
static constexpr result_type multiplier = a;
static constexpr result_type increment = c;
static constexpr result_type modulus = m;
static constexpr result_type min() { return c == 0u ? 1u: 0u; }
static constexpr result_type max() { return m - 1u; }
static constexpr result_type default_seed = 1u;
// constructors and seeding functions
explicit linear_congruential_engine(result_type s = default_seed);
template<class Sseq> explicit linear_congruential_engine(Sseq& q);
void seed(result_type s = default_seed);
template<class Sseq> void seed(Sseq& q);
// generating functions
result_type operator()();
void discard(unsigned long long z);
};
If the template parameter m is 0, the modulus m used throughout this section [rand.eng.lcong] is numeric_limits<result_type>::max() plus 1. [ Note: m need not be representable as a value of type result_type. — end note ]
If the template parameter m is not 0, the following relations shall hold: a < m and c < m.
The textual representation consists of the value of xi.
explicit linear_congruential_engine(result_type s = default_seed);
Effects: Constructs a linear_congruential_engine object. If c mod m is 0 and s mod m is 0, sets the engine's state to 1, otherwise sets the engine's state to s mod m.
template<class Sseq> explicit linear_congruential_engine(Sseq& q);
Effects: Constructs a linear_congruential_engine object.
With
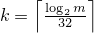 and a an array (or equivalent)
of length k + 3,
invokes q.generate(a+0, a+k+3)
and then computes
and a an array (or equivalent)
of length k + 3,
invokes q.generate(a+0, a+k+3)
and then computes
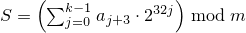 .
If
c mod m is 0
and
S is 0,
sets the engine's state to 1,
else sets the engine's state
to S.
.
If
c mod m is 0
and
S is 0,
sets the engine's state to 1,
else sets the engine's state
to S.
26.5.3.2 Class template mersenne_twister_engine [rand.eng.mers]
A mersenne_twister_engine random number engine276 produces unsigned integer random numbers in the closed interval [0,2w-1]. The state xi of a mersenne_twister_engine object x is of size n and consists of a sequence X of n values of the type delivered by x; all subscripts applied to X are to be taken modulo n.
The transition algorithm employs a twisted generalized feedback shift register defined by shift values n and m, a twist value r, and a conditional xor-mask a. To improve the uniformity of the result, the bits of the raw shift register are additionally tempered (i.e., scrambled) according to a bit-scrambling matrix defined by values u, d, s, b, t, c, and ℓ.
The state transition is performed as follows:
Concatenate the upper w-r bits of Xi-n with the lower r bits of Xi+1-n to obtain an unsigned integer value Y.
With α = a · (Y bitand 1), set Xi to Xi+m-n xor (Y rshift 1) xor α.
The sequence X is initialized with the help of an initialization multiplier f.
The generation algorithm determines the unsigned integer values z1, z2, z3, z4 as follows, then delivers z4 as its result:
Let z1 = Xi xor (( Xi rshift u ) bitand d).
Let z2 = z1 xor ( (z1 lshiftw s) bitand b ).
Let z3 = z2 xor ( (z2 lshiftw t) bitand c ).
Let z4 = z3 xor ( z3 rshift ℓ ).
template<class UIntType, size_t w, size_t n, size_t m, size_t r,
UIntType a, size_t u, UIntType d, size_t s,
UIntType b, size_t t,
UIntType c, size_t l, UIntType f>
class mersenne_twister_engine{
public:
// types
typedef UIntType result_type;
// engine characteristics
static constexpr size_t word_size = w;
static constexpr size_t state_size = n;
static constexpr size_t shift_size = m;
static constexpr size_t mask_bits = r;
static constexpr UIntType xor_mask = a;
static constexpr size_t tempering_u = u;
static constexpr UIntType tempering_d = d;
static constexpr size_t tempering_s = s;
static constexpr UIntType tempering_b = b;
static constexpr size_t tempering_t = t;
static constexpr UIntType tempering_c = c;
static constexpr size_t tempering_l = l;
static constexpr UIntType initialization_multiplier = f;
static constexpr result_type min() { return 0; }
static constexpr result_type max() { return 2w - 1; }
static constexpr result_type default_seed = 5489u;
// constructors and seeding functions
explicit mersenne_twister_engine(result_type value = default_seed);
template<class Sseq> explicit mersenne_twister_engine(Sseq& q);
void seed(result_type value = default_seed);
template<class Sseq> void seed(Sseq& q);
// generating functions
result_type operator()();
void discard(unsigned long long z);
};
The following relations shall hold: 0 < m, m <= n, 2u < w, r <= w, u <= w, s <= w, t <= w, l <= w, w <= numeric_limits<UIntType>::digits, a <= (1u<<w) - 1u, b <= (1u<<w) - 1u, c <= (1u<<w) - 1u, d <= (1u<<w) - 1u, and f <= (1u<<w) - 1u.
The textual representation of xi consists of the values of Xi-n, …, Xi-1, in that order.
explicit mersenne_twister_engine(result_type value = default_seed);
Effects: Constructs a mersenne_twister_engine object. Sets X-n to value mod 2w. Then, iteratively for i = 1-n,…,-1, sets Xi to [f · (Xi-1 xor (Xi-1 rshift (w-2)) ) + i mod n ] mod 2w .
Complexity: Ο(n).
template<class Sseq> explicit mersenne_twister_engine(Sseq& q);
Effects: Constructs a mersenne_twister_engine object.
With
k = ⌈ w / 32 ⌉
and a an array (or equivalent)
of length n · k ,
invokes q.generate(a+0, a+n · k)
and then, iteratively for i = -n,…,-1,
sets Xi
to 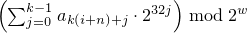 .
Finally,
if the most significant w-r bits of X-n
are zero,
and if each of the other resulting Xi is 0,
changes X-n
to 2w-1 .
.
Finally,
if the most significant w-r bits of X-n
are zero,
and if each of the other resulting Xi is 0,
changes X-n
to 2w-1 .
The name of this engine refers, in part, to a property of its period: For properly-selected values of the parameters, the period is closely related to a large Mersenne prime number.
26.5.3.3 Class template subtract_with_carry_engine [rand.eng.sub]
A subtract_with_carry_engine random number engine produces unsigned integer random numbers.
The state xi of a subtract_with_carry_engine object x is of size Ο(r), and consists of a sequence X of r integer values 0 ≤ Xi < m = 2w; all subscripts applied to X are to be taken modulo r. The state xi additionally consists of an integer c (known as the carry) whose value is either 0 or 1.
The state transition is performed as follows:
Let Y = Xi-s - Xi-r - c .
Set Xi to y = Y mod m . Set c to 1 if Y < 0, otherwise set c to 0.
[ Note: This algorithm corresponds to a modular linear function of the form TA(xi) = (a · xi) mod b , where b is of the form mr - ms + 1 and a = b - (b-1) / m . — end note ]
The generation algorithm is given by GA(xi) = y , where y is the value produced as a result of advancing the engine's state as described above.
template<class UIntType, size_t w, size_t s, size_t r>
class subtract_with_carry_engine{
public:
// types
typedef UIntType result_type;
// engine characteristics
static constexpr size_t word_size = w;
static constexpr size_t short_lag = s;
static constexpr size_t long_lag = r;
static constexpr result_type min() { return 0; }
static constexpr result_type max() { return m - 1; }
static constexpr result_type default_seed = 19780503u;
// constructors and seeding functions
explicit subtract_with_carry_engine(result_type value = default_seed);
template<class Sseq> explicit subtract_with_carry_engine(Sseq& q);
void seed(result_type value = default_seed);
template<class Sseq> void seed(Sseq& q);
// generating functions
result_type operator()();
void discard(unsigned long long z);
};
The following relations shall hold: 0u < s, s < r, 0 < w, and w <= numeric_limits<UIntType>::digits.
The textual representation consists of the values of Xi-r, …, Xi-1, in that order, followed by c.
explicit subtract_with_carry_engine(result_type value = default_seed);
Effects: Constructs a subtract_with_carry_engine object. Sets the values of X-r, …, X-1 , in that order, as specified below. If X-1 is then 0, sets c to 1; otherwise sets c to 0.
To set the values Xk, first construct e, a linear_congruential_engine object, as if by the following definition:
linear_congruential_engine<result_type,
40014u,0u,2147483563u> e(value == 0u ? default_seed : value);
Then, to set each Xk,
obtain new values z0, …, zn-1
from n = ⌈ w/32 ⌉ successive invocations
of e taken modulo 232.
Set Xk to 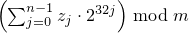 .
.
Complexity: Exactly n · r invocations of e.
template<class Sseq> explicit subtract_with_carry_engine(Sseq& q);
Effects: Constructs a subtract_with_carry_engine object.
With
k = ⌈ w / 32 ⌉
and a an array (or equivalent)
of length r · k ,
invokes q.generate(a+0, a+r · k)
and then, iteratively for i = -r, …, -1,
sets Xi
to 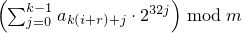 .
If X-1 is then 0,
sets c to 1;
otherwise sets c to 0.
.
If X-1 is then 0,
sets c to 1;
otherwise sets c to 0.
26.5.4 Random number engine adaptor class templates [rand.adapt]
26.5.4.1 In general [rand.adapt.general]
Each type instantiated from a class template specified in this section [rand.eng] satisfies the requirements of a random number engine adaptor ([rand.req.adapt]) type.
Except where specified otherwise, the complexity of each function specified in this section [rand.adapt] is constant.
Except where specified otherwise, no function described in this section [rand.adapt] throws an exception.
Descriptions are provided in this section [rand.adapt] only for adaptor operations that are not described in section [rand.req.adapt] or for operations where there is additional semantic information. In particular, declarations for copy constructors, for copy assignment operators, for streaming operators, and for equality and inequality operators are not shown in the synopses.
Each template specified in this section [rand.adapt] requires one or more relationships, involving the value(s) of its non-type template parameter(s), to hold. A program instantiating any of these templates is ill-formed if any such required relationship fails to hold.
26.5.4.2 Class template discard_block_engine [rand.adapt.disc]
A discard_block_engine random number engine adaptor produces random numbers selected from those produced by some base engine e. The state xi of a discard_block_engine engine adaptor object x consists of the state ei of its base engine e and an additional integer n. The size of the state is the size of e's state plus 1.
The transition algorithm discards all but r > 0 values from each block of p ≥ r values delivered by e. The state transition is performed as follows: If n ≥ r, advance the state of e from ei to ei+p-r and set n to 0. In any case, then increment n and advance e's then-current state ej to ej+1.
The generation algorithm yields the value returned by the last invocation of e() while advancing e's state as described above.
template<class Engine, size_t p, size_t r>
class discard_block_engine{
public:
// types
typedef typename Engine::result_type result_type;
// engine characteristics
static constexpr size_t block_size = p;
static constexpr size_t used_block = r;
static constexpr result_type min() { return Engine::min(); }
static constexpr result_type max() { return Engine::max(); }
// constructors and seeding functions
discard_block_engine();
explicit discard_block_engine(const Engine& e);
explicit discard_block_engine(Engine&& e);
explicit discard_block_engine(result_type s);
template<class Sseq> explicit discard_block_engine(Sseq& q);
void seed();
void seed(result_type s);
template<class Sseq> void seed(Sseq& q);
// generating functions
result_type operator()();
void discard(unsigned long long z);
// property functions
const Engine& base() const noexcept { return e; };
private:
Engine e; // exposition only
int n; // exposition only
};
The following relations shall hold: 0 < r and r <= p.
In addition to its behavior pursuant to section [rand.req.adapt], each constructor that is not a copy constructor sets n to 0.
26.5.4.3 Class template independent_bits_engine [rand.adapt.ibits]
An independent_bits_engine random number engine adaptor combines random numbers that are produced by some base engine e, so as to produce random numbers with a specified number of bits w. The state xi of an independent_bits_engine engine adaptor object x consists of the state ei of its base engine e; the size of the state is the size of e's state.
The transition and generation algorithms are described in terms of the following integral constants:
Let R = e.max() - e.min() + 1 and m = ⌊ log2 R ⌋ .
With n as determined below, let w0 = ⌊ w / n ⌋ , n0 = n - w mod n , y0 = 2w0 ⌊ R / 2w0 ⌋ , and y1 = 2w0 + 1 ⌊ R / 2w0 + 1 ⌋ .
Let n = ⌈ w / m ⌉ if and only if the relation R - y0 ≤ ⌊ y0 / n ⌋ holds as a result. Otherwise let n = 1 + ⌈ w / m ⌉ .
[ Note: The relation w = n0 w0 + (n - n0)(w0 + 1) always holds. — end note ]
The transition algorithm is carried out by invoking e() as often as needed to obtain n0 values less than y0 + e.min() and n - n0 values less than y1 + e.min() .
The generation algorithm uses the values produced while advancing the state as described above to yield a quantity S obtained as if by the following algorithm:
S = 0; for (k = 0; k ≠ n0; k += 1) { do u = e() - e.min(); while ( u ≥ y0 ); S = 2w0 · S + u mod 2w0 ; } for (k = n0; k ≠ n; k += 1) { do u = e() - e.min(); while ( u ≥ y1 ); S = 2w0 + 1 · S + u mod 2w0 + 1 ; }
template<class Engine, size_t w, class UIntType>
class independent_bits_engine{
public:
// types
typedef UIntType result_type;
// engine characteristics
static constexpr result_type min() { return 0; }
static constexpr result_type max() { return 2w - 1; }
// constructors and seeding functions
independent_bits_engine();
explicit independent_bits_engine(const Engine& e);
explicit independent_bits_engine(Engine&& e);
explicit independent_bits_engine(result_type s);
template<class Sseq> explicit independent_bits_engine(Sseq& q);
void seed();
void seed(result_type s);
template<class Sseq> void seed(Sseq& q);
// generating functions
result_type operator()();
void discard(unsigned long long z);
// property functions
const Engine& base() const noexcept { return e; };
private:
Engine e; // exposition only
};
The following relations shall hold: 0 < w and w <= numeric_limits<result_type>::digits.
26.5.4.4 Class template shuffle_order_engine [rand.adapt.shuf]
A shuffle_order_engine random number engine adaptor produces the same random numbers that are produced by some base engine e, but delivers them in a different sequence. The state xi of a shuffle_order_engine engine adaptor object x consists of the state ei of its base engine e, an additional value Y of the type delivered by e, and an additional sequence V of k values also of the type delivered by e. The size of the state is the size of e's state plus k+1.
The transition algorithm permutes the values produced by e. The state transition is performed as follows:
Calculate an integer
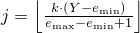 .
.
Set Y to Vj and then set Vj to e().
The generation algorithm yields the last value of Y produced while advancing e's state as described above.
template<class Engine, size_t k>
class shuffle_order_engine{
public:
// types
typedef typename Engine::result_type result_type;
// engine characteristics
static constexpr size_t table_size = k;
static constexpr result_type min() { return Engine::min(); }
static constexpr result_type max() { return Engine::max(); }
// constructors and seeding functions
shuffle_order_engine();
explicit shuffle_order_engine(const Engine& e);
explicit shuffle_order_engine(Engine&& e);
explicit shuffle_order_engine(result_type s);
template<class Sseq> explicit shuffle_order_engine(Sseq& q);
void seed();
void seed(result_type s);
template<class Sseq> void seed(Sseq& q);
// generating functions
result_type operator()();
void discard(unsigned long long z);
// property functions
const Engine& base() const noexcept { return e; };
private:
Engine e; // exposition only
result_type Y; // exposition only
result_type V[k]; // exposition only
};
The following relation shall hold: 0 < k.
The textual representation consists of the textual representation of e, followed by the k values of V, followed by the value of Y.
In addition to its behavior pursuant to section [rand.req.adapt], each constructor that is not a copy constructor initializes V[0], …, V[k-1] and Y, in that order, with values returned by successive invocations of e().
26.5.5 Engines and engine adaptors with predefined parameters [rand.predef]
typedef linear_congruential_engine<uint_fast32_t, 16807, 0, 2147483647>
minstd_rand0;
Required behavior: The 10000 th consecutive invocation of a default-constructed object of type minstd_rand0 shall produce the value 1043618065.
typedef linear_congruential_engine<uint_fast32_t, 48271, 0, 2147483647>
minstd_rand;
Required behavior: The 10000 th consecutive invocation of a default-constructed object of type minstd_rand shall produce the value 399268537.
typedef mersenne_twister_engine<uint_fast32_t,
32,624,397,31,0x9908b0df,11,0xffffffff,7,0x9d2c5680,15,0xefc60000,18,1812433253>
mt19937;
Required behavior: The 10000 th consecutive invocation of a default-constructed object of type mt19937 shall produce the value 4123659995.
typedef mersenne_twister_engine<uint_fast64_t,
64,312,156,31,0xb5026f5aa96619e9,29,
0x5555555555555555,17,
0x71d67fffeda60000,37,
0xfff7eee000000000,43,
6364136223846793005>
mt19937_64;
Required behavior: The 10000 th consecutive invocation of a default-constructed object of type mt19937_64 shall produce the value 9981545732273789042.
typedef subtract_with_carry_engine<uint_fast32_t, 24, 10, 24>
ranlux24_base;
Required behavior: The 10000 th consecutive invocation of a default-constructed object of type ranlux24_base shall produce the value 7937952 .
typedef subtract_with_carry_engine<uint_fast64_t, 48, 5, 12>
ranlux48_base;
Required behavior: The 10000 th consecutive invocation of a default-constructed object of type ranlux48_base shall produce the value 61839128582725 .
typedef discard_block_engine<ranlux24_base, 223, 23>
ranlux24;
Required behavior: The 10000 th consecutive invocation of a default-constructed object of type ranlux24 shall produce the value 9901578 .
typedef discard_block_engine<ranlux48_base, 389, 11>
ranlux48;
Required behavior: The 10000 th consecutive invocation of a default-constructed object of type ranlux48 shall produce the value 249142670248501 .
typedef shuffle_order_engine<minstd_rand0,256>
knuth_b;
Required behavior: The 10000 th consecutive invocation of a default-constructed object of type knuth_b shall produce the value 1112339016.
typedef implementation-defined
default_random_engine;
Remark: The choice of engine type named by this typedef is implementation-defined. [ Note: The implementation may select this type on the basis of performance, size, quality, or any combination of such factors, so as to provide at least acceptable engine behavior for relatively casual, inexpert, and/or lightweight use. Because different implementations may select different underlying engine types, code that uses this typedef need not generate identical sequences across implementations. — end note ]
26.5.6 Class random_device [rand.device]
A random_device uniform random number generator produces non-deterministic random numbers.
If implementation limitations prevent generating non-deterministic random numbers, the implementation may employ a random number engine.
class random_device{
public:
// types
typedef unsigned int result_type;
// generator characteristics
static constexpr result_type min() { return numeric_limits<result_type>::min(); }
static constexpr result_type max() { return numeric_limits<result_type>::max(); }
// constructors
explicit random_device(const string& token = implementation-defined);
// generating functions
result_type operator()();
// property functions
double entropy() const noexcept;
// no copy functions
random_device(const random_device& ) = delete;
void operator=(const random_device& ) = delete;
};
explicit random_device(const string& token = implementation-defined);
Effects: Constructs a random_device non-deterministic uniform random number generator object. The semantics and default value of the token parameter are implementation-defined.277
Throws: A value of an implementation-defined type derived from exception if the random_device could not be initialized.
double entropy() const noexcept;
Returns: If the implementation employs a random number engine, returns 0.0. Otherwise, returns an entropy estimate278 for the random numbers returned by operator(), in the range min() to log2( max()+1).
Returns: A non-deterministic random value, uniformly distributed between min() and max(), inclusive. It is implementation-defined how these values are generated.
Throws: A value of an implementation-defined type derived from exception if a random number could not be obtained.
The parameter is intended to allow an implementation to differentiate between different sources of randomness.
If a device has n states
whose respective probabilities are
P0, …, Pn-1 ,
the device entropy S is defined as
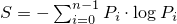 .
.
26.5.7 Utilities [rand.util]
26.5.7.1 Class seed_seq [rand.util.seedseq]
class seed_seq{
public:
// types
typedef uint_least32_t result_type;
// constructors
seed_seq();
template<class T>
seed_seq(initializer_list<T> il);
template<class InputIterator>
seed_seq(InputIterator begin, InputIterator end);
// generating functions
template<class RandomAccessIterator>
void generate(RandomAccessIterator begin, RandomAccessIterator end);
// property functions
size_t size() const;
template<class OutputIterator>
void param(OutputIterator dest) const;
// no copy functions
seed_seq(const seed_seq& ) = delete;
void operator=(const seed_seq& ) = delete;
private:
vector<result_type> v; // exposition only
};
Effects: Constructs a seed_seq object as if by default-constructing its member v.
Throws: Nothing.
template<class T>
seed_seq(initializer_list<T> il);
Requires: T shall be an integer type.
Effects: Same as seed_seq(il.begin(), il.end()).
template<class InputIterator>
seed_seq(InputIterator begin, InputIterator end);
Requires: InputIterator shall satisfy the requirements of an input iterator (Table [tab:iterator.input.requirements]) type. Moreover, iterator_traits<InputIterator>::value_type shall denote an integer type.
Effects: Constructs a seed_seq object by the following algorithm:
for( InputIterator s = begin; s != end; ++s)
v.push_back((*s)mod 232);
template<class RandomAccessIterator>
void generate(RandomAccessIterator begin, RandomAccessIterator end);
Requires: RandomAccessIterator shall meet the requirements of a mutable random access iterator (Table [tab:iterator.random.access.requirements]) type. Moreover, iterator_traits<RandomAccessIterator>::value_type shall denote an unsigned integer type capable of accommodating 32-bit quantities.
Effects: Does nothing if begin == end. Otherwise, with s = v.size() and n = end - begin , fills the supplied range [begin,end) according to the following algorithm in which each operation is to be carried out modulo 232, each indexing operator applied to begin is to be taken modulo n, and T(x) is defined as x xor (x rshift 27):
By way of initialization, set each element of the range to the value 0x8b8b8b8b. Additionally, for use in subsequent steps, let p = (n - t) / 2 and let q = p + t, where t = (n ≥ 623) ? 11 : (n ≥ 68) ? 7 : (n ≥ 39) ? 5 : (n ≥ 7) ? 3 : (n - 1)/2;
With m as the larger of s + 1 and n, transform the elements of the range: iteratively for k = 0, …, m-1 , calculate values
![\begin{eqnarray*}
r_1 & = &
1664525 \cdot \texttt{T}\left( \texttt{begin[}k\texttt{]}
\ensuremath{\, \mathsf{xor} \,} \texttt{begin[}k+p\texttt{]}
\ensuremath{\, \mathsf{xor} \,} \texttt{begin[}k-1 \texttt{]}
\right)
\\
r_2 & = & r_1 + \left\{
\begin{array}{cl}
s & \mbox{, } k = 0
\\
k \bmod n + \texttt{v[}k-1\texttt{]} & \mbox{, } 0 < k \le s
\\
k \bmod n & \mbox{, } s < k
\end{array}
\right.
\end{eqnarray*}](math/5460180720864397012.png) and, in order,
increment begin[k+p] by r1,
increment begin[k+q] by r2,
and
set begin[k] to r2.
and, in order,
increment begin[k+p] by r1,
increment begin[k+q] by r2,
and
set begin[k] to r2.
Transform the elements of the range again, beginning where the previous step ended: iteratively for k = m, …, m+n-1 , calculate values
![\begin{eqnarray*}
r_3 & = &
1566083941 \cdot \texttt{T}\left( \texttt{begin[}k \texttt{]}
+ \texttt{begin[}k+p\texttt{]}
+ \texttt{begin[}k-1\texttt{]}
\right)
\\
r_4 & = & r_3 - (k \bmod n)
\end{eqnarray*}](math/5265029910326981193.png) and, in order,
update begin[k+p] by xoring it with r3,
update begin[k+q] by xoring it with r4,
and
set begin[k] to r4.
and, in order,
update begin[k+p] by xoring it with r3,
update begin[k+q] by xoring it with r4,
and
set begin[k] to r4.
Throws: What and when RandomAccessIterator operations of begin and end throw.
Returns: The number of 32-bit units that would be returned by a call to param().
Throws: Nothing.
Complexity: Constant time.
template<class OutputIterator>
void param(OutputIterator dest) const;
Requires: OutputIterator shall satisfy the requirements of an output iterator (Table [tab:iterator.output.requirements]) type. Moreover, the expression *dest = rt shall be valid for a value rt of type result_type.
Effects: Copies the sequence of prepared 32-bit units to the given destination, as if by executing the following statement:
copy(v.begin(), v.end(), dest);
Throws: What and when OutputIterator operations of dest throw.
26.5.7.2 Function template generate_canonical [rand.util.canonical]
Each function instantiated from the template described in this section [rand.util.canonical] maps the result of one or more invocations of a supplied uniform random number generator g to one member of the specified RealType such that, if the values gi produced by g are uniformly distributed, the instantiation's results tj, 0 ≤ tj < 1 , are distributed as uniformly as possible as specified below.
[ Note: Obtaining a value in this way can be a useful step in the process of transforming a value generated by a uniform random number generator into a value that can be delivered by a random number distribution. — end note ]
template<class RealType, size_t bits, class URNG>
RealType generate_canonical(URNG& g);
Complexity: Exactly k = max(1, ⌈ b / log2 R ⌉) invocations of g, where b279 is the lesser of numeric_limits<RealType>::digits and bits, and R is the value of g.max() - g.min() + 1 .
Effects:
Invokes g() k times
to obtain values g0, …, gk-1 , respectively.
Calculates a quantity
![\[
S = \sum_{i=0}^{k-1} (g_i - \texttt{g.min()})
\cdot R^i
\]](math/1815020361946892378.png) using arithmetic of type
RealType.
using arithmetic of type
RealType.
Returns: S / Rk .
Throws: What and when g throws.
b is introduced to avoid any attempt to produce more bits of randomness than can be held in RealType.
26.5.8 Random number distribution class templates [rand.dist]
26.5.8.1 In general [rand.dist.general]
Each type instantiated from a class template specified in this section [rand.dist] satisfies the requirements of a random number distribution ([rand.req.dist]) type.
Descriptions are provided in this section [rand.dist] only for distribution operations that are not described in [rand.req.dist] or for operations where there is additional semantic information. In particular, declarations for copy constructors, for copy assignment operators, for streaming operators, and for equality and inequality operators are not shown in the synopses.
The algorithms for producing each of the specified distributions are implementation-defined.
The value of each probability density function p(z) and of each discrete probability function P(zi) specified in this section is 0 everywhere outside its stated domain.
26.5.8.2 Uniform distributions [rand.dist.uni]
26.5.8.2.1 Class template uniform_int_distribution [rand.dist.uni.int]
A uniform_int_distribution random number distribution produces random integers i, a ≤ i ≤ b , distributed according to the constant discrete probability function P(i | a,b) = 1 / (b - a + 1) .
template<class IntType = int>
class uniform_int_distribution{
public:
// types
typedef IntType result_type;
typedef unspecified param_type;
// constructors and reset functions
explicit uniform_int_distribution(IntType a = 0, IntType b = numeric_limits<IntType>::max());
explicit uniform_int_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
result_type a() const;
result_type b() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit uniform_int_distribution(IntType a = 0, IntType b = numeric_limits<IntType>::max());
Requires: a ≤ b .
Effects: Constructs a uniform_int_distribution object; a and b correspond to the respective parameters of the distribution.
Returns: The value of the a parameter with which the object was constructed.
Returns: The value of the b parameter with which the object was constructed.
26.5.8.2.2 Class template uniform_real_distribution [rand.dist.uni.real]
A uniform_real_distribution random number distribution produces random numbers x, a ≤ x < b , distributed according to the constant probability density function p(x | a,b) = 1 / (b - a) .
template<class RealType = double>
class uniform_real_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructors and reset functions
explicit uniform_real_distribution(RealType a = 0.0, RealType b = 1.0);
explicit uniform_real_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
result_type a() const;
result_type b() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit uniform_real_distribution(RealType a = 0.0, RealType b = 1.0);
Requires: a ≤ b and b - a ≤ numeric_limits<RealType>::max() .
Effects: Constructs a uniform_real_distribution object; a and b correspond to the respective parameters of the distribution.
Returns: The value of the a parameter with which the object was constructed.
Returns: The value of the b parameter with which the object was constructed.
26.5.8.3 Bernoulli distributions [rand.dist.bern]
26.5.8.3.1 Class bernoulli_distribution [rand.dist.bern.bernoulli]
A bernoulli_distribution random number distribution
produces bool values b
distributed according to
the discrete probability function
![\[%
P(b\,|\,p)
= \left\{ \begin{array}{lcl}
p & \mbox{if} & b = \texttt{true} \\
1-p & \mbox{if} & b = \texttt{false}
\end{array}\right.
\; \mbox{.}
\]](math/5980848140442699116.png)
class bernoulli_distribution{
public:
// types
typedef bool result_type;
typedef unspecified param_type;
// constructors and reset functions
explicit bernoulli_distribution(double p = 0.5);
explicit bernoulli_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
double p() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
Requires: 0 ≤ p ≤ 1.
Effects: Constructs a bernoulli_distribution object; p corresponds to the parameter of the distribution.
Returns: The value of the p parameter with which the object was constructed.
26.5.8.3.2 Class template binomial_distribution [rand.dist.bern.bin]
A binomial_distribution random number distribution
produces integer values i ≥ 0
distributed according to
the discrete probability function
![\[%
P(i\,|\,t,p)
= \binom{t}{i} \cdot p^i \cdot (1-p)^{t-i}
\; \mbox{.}
\]](math/1013655488086605659.png)
template<class IntType = int>
class binomial_distribution{
public:
// types
typedef IntType result_type;
typedef unspecified param_type;
// constructors and reset functions
explicit binomial_distribution(IntType t = 1, double p = 0.5);
explicit binomial_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
IntType t() const;
double p() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit binomial_distribution(IntType t = 1, double p = 0.5);
Requires: 0 ≤ p ≤ 1 and 0 ≤ t .
Effects: Constructs a binomial_distribution object; t and p correspond to the respective parameters of the distribution.
Returns: The value of the t parameter with which the object was constructed.
Returns: The value of the p parameter with which the object was constructed.
26.5.8.3.3 Class template geometric_distribution [rand.dist.bern.geo]
A geometric_distribution random number distribution produces integer values i ≥ 0 distributed according to the discrete probability function P(i | p) = p · (1-p)i .
template<class IntType = int>
class geometric_distribution{
public:
// types
typedef IntType result_type;
typedef unspecified param_type;
// constructors and reset functions
explicit geometric_distribution(double p = 0.5);
explicit geometric_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
double p() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
Requires: 0 < p < 1.
Effects: Constructs a geometric_distribution object; p corresponds to the parameter of the distribution.
Returns: The value of the p parameter with which the object was constructed.
26.5.8.3.4 Class template negative_binomial_distribution [rand.dist.bern.negbin]
A negative_binomial_distribution random number distribution
produces random integers i ≥ 0
distributed according to
the discrete probability function
![\[%
P(i\,|\,k,p)
= \binom{k+i-1}{i} \cdot p^k \cdot (1-p)^i
\; \mbox{.}
\]](math/7350092705052863326.png)
template<class IntType = int>
class negative_binomial_distribution{
public:
// types
typedef IntType result_type;
typedef unspecified param_type;
// constructor and reset functions
explicit negative_binomial_distribution(IntType k = 1, double p = 0.5);
explicit negative_binomial_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
IntType k() const;
double p() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit negative_binomial_distribution(IntType k = 1, double p = 0.5);
Requires: 0 < p ≤ 1 and 0 < k .
Effects: Constructs a negative_binomial_distribution object; k and p correspond to the respective parameters of the distribution.
Returns: The value of the k parameter with which the object was constructed.
Returns: The value of the p parameter with which the object was constructed.
26.5.8.4 Poisson distributions [rand.dist.pois]
26.5.8.4.1 Class template poisson_distribution [rand.dist.pois.poisson]
A poisson_distribution random number distribution
produces integer values i ≥ 0
distributed according to
the discrete probability function
![\[%
P(i\,|\,\mu)
= \frac{ e^{-\mu} \mu^{i} }
{ i\,! }
\; \mbox{.}
\]](math/8063431532719405600.png) The distribution parameter μ
is also known as this distribution's mean.
The distribution parameter μ
is also known as this distribution's mean.
template<class IntType = int>
class poisson_distribution{
public:
// types
typedef IntType result_type;
typedef unspecified param_type;
// constructors and reset functions
explicit poisson_distribution(double mean = 1.0);
explicit poisson_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
double mean() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
Requires: 0 < mean .
Effects: Constructs a poisson_distribution object; mean corresponds to the parameter of the distribution.
Returns: The value of the mean parameter with which the object was constructed.
26.5.8.4.2 Class template exponential_distribution [rand.dist.pois.exp]
An exponential_distribution random number distribution produces random numbers x > 0 distributed according to the probability density function p(x | λ) = λ e-λ x .
template<class RealType = double>
class exponential_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructors and reset functions
explicit exponential_distribution(RealType lambda = 1.0);
explicit exponential_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
RealType lambda() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
Requires: 0 < lambda .
Effects: Constructs a exponential_distribution object; lambda corresponds to the parameter of the distribution.
Returns: The value of the lambda parameter with which the object was constructed.
26.5.8.4.3 Class template gamma_distribution [rand.dist.pois.gamma]
A gamma_distribution random number distribution
produces random numbers x > 0
distributed according to
the probability density function
![\[%
p(x\,|\,\alpha,\beta)
= \frac{e^{-x/\beta}}{\beta^{\alpha} \cdot \Gamma(\alpha)}
\, \cdot \, x^{\, \alpha-1}
\; \mbox{.}
\]](math/2818784873481647269.png)
template<class RealType = double>
class gamma_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructors and reset functions
explicit gamma_distribution(RealType alpha = 1.0, RealType beta = 1.0);
explicit gamma_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
RealType alpha() const;
RealType beta() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit gamma_distribution(RealType alpha = 1.0, RealType beta = 1.0);
Requires: 0 < alpha and 0 < beta .
Effects: Constructs a gamma_distribution object; alpha and beta correspond to the parameters of the distribution.
Returns: The value of the alpha parameter with which the object was constructed.
Returns: The value of the beta parameter with which the object was constructed.
26.5.8.4.4 Class template weibull_distribution [rand.dist.pois.weibull]
A weibull_distribution random number distribution
produces random numbers x ≥ 0
distributed according to
the probability density function
![\[%
p(x\,|\,a,b)
= \frac{a}{b}
\cdot \left(\frac{x}{b}\right)^{a-1}
\cdot \, \exp\left( -\left(\frac{x}{b}\right)^a\right)
\; \mbox{.}
\]](math/7851113081917117550.png)
template<class RealType = double>
class weibull_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructor and reset functions
explicit weibull_distribution(RealType a = 1.0, RealType b = 1.0);
explicit weibull_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
RealType a() const;
RealType b() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit weibull_distribution(RealType a = 1.0, RealType b = 1.0);
Requires: 0 < a and 0 < b .
Effects: Constructs a weibull_distribution object; a and b correspond to the respective parameters of the distribution.
Returns: The value of the a parameter with which the object was constructed.
Returns: The value of the b parameter with which the object was constructed.
26.5.8.4.5 Class template extreme_value_distribution [rand.dist.pois.extreme]
An extreme_value_distribution random number distribution
produces random numbers x
distributed according to
the probability density function280
![\[%
p(x\,|\,a,b)
= \frac{1}{b}
\cdot \exp\left( \frac{a-x}{b}
\,-\, \exp\left(\frac{a-x}{b}\right)
\right)
\; \mbox{.}
\]](math/1314498286204533439.png)
template<class RealType = double>
class extreme_value_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructor and reset functions
explicit extreme_value_distribution(RealType a = 0.0, RealType b = 1.0);
explicit extreme_value_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
RealType a() const;
RealType b() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit extreme_value_distribution(RealType a = 0.0, RealType b = 1.0);
Requires: 0 < b .
Effects: Constructs an extreme_value_distribution object; a and b correspond to the respective parameters of the distribution.
Returns: The value of the a parameter with which the object was constructed.
Returns: The value of the b parameter with which the object was constructed.
The distribution corresponding to this probability density function is also known (with a possible change of variable) as the Gumbel Type I, the log-Weibull, or the Fisher-Tippett Type I distribution.
26.5.8.5 Normal distributions [rand.dist.norm]
26.5.8.5.1 Class template normal_distribution [rand.dist.norm.normal]
A normal_distribution random number distribution
produces random numbers x
distributed according to
the probability density function
![\[%
p(x\,|\,\mu,\sigma)
= \frac{1}{\sigma \sqrt{2\pi}}
\cdot
% e^{-(x-\mu)^2 / (2\sigma^2)}
\exp{\left(- \, \frac{(x - \mu)^2}
{2 \sigma^2}
\right)
}
\; \mbox{.}
\]](math/1317982862401636365.png) The distribution parameters μ and σ
are also known as this distribution's mean
and standard deviation.
The distribution parameters μ and σ
are also known as this distribution's mean
and standard deviation.
template<class RealType = double>
class normal_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructors and reset functions
explicit normal_distribution(RealType mean = 0.0, RealType stddev = 1.0);
explicit normal_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
RealType mean() const;
RealType stddev() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit normal_distribution(RealType mean = 0.0, RealType stddev = 1.0);
Requires: 0 < stddev .
Effects: Constructs a normal_distribution object; mean and stddev correspond to the respective parameters of the distribution.
Returns: The value of the mean parameter with which the object was constructed.
Returns: The value of the stddev parameter with which the object was constructed.
26.5.8.5.2 Class template lognormal_distribution [rand.dist.norm.lognormal]
A lognormal_distribution random number distribution
produces random numbers x > 0
distributed according to
the probability density function
![\[%
p(x\,|\,m,s)
= \frac{1}
{s x \sqrt{2 \pi}}
\cdot
\exp{\left(- \, \frac{(\ln{x} - m)^2}
{2 s^2}
\right)
}
\; \mbox{.}
\]](math/2696700243271672895.png)
template<class RealType = double>
class lognormal_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructor and reset functions
explicit lognormal_distribution(RealType m = 0.0, RealType s = 1.0);
explicit lognormal_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
RealType m() const;
RealType s() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit lognormal_distribution(RealType m = 0.0, RealType s = 1.0);
Requires: 0 < s .
Effects: Constructs a lognormal_distribution object; m and s correspond to the respective parameters of the distribution.
Returns: The value of the m parameter with which the object was constructed.
Returns: The value of the s parameter with which the object was constructed.
26.5.8.5.3 Class template chi_squared_distribution [rand.dist.norm.chisq]
A chi_squared_distribution random number distribution
produces random numbers x>0
distributed according to
the probability density function
![\[%
p(x\,|\,n)
= \frac{ x^{(n/2)-1} \cdot e^{-x/2}}
{\Gamma(n/2) \cdot 2^{n/2}}
\; \mbox{.}
\]](math/6635143828116624469.png)
template<class RealType = double>
class chi_squared_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructor and reset functions
explicit chi_squared_distribution(RealType n = 1);
explicit chi_squared_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
RealType n() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
Requires: 0 < n .
Effects: Constructs a chi_squared_distribution object; n corresponds to the parameter of the distribution.
Returns: The value of the n parameter with which the object was constructed.
26.5.8.5.4 Class template cauchy_distribution [rand.dist.norm.cauchy]
A cauchy_distribution random number distribution
produces random numbers x
distributed according to
the probability density function
![\[%
p(x\,|\,a,b)
= \left( \pi b \left( 1 + \left( \frac{x-a}{b} \right)^2 \;\right)\right)^{-1}
\; \mbox{.}
\]](math/822148464658683675.png)
template<class RealType = double>
class cauchy_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructor and reset functions
explicit cauchy_distribution(RealType a = 0.0, RealType b = 1.0);
explicit cauchy_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
RealType a() const;
RealType b() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit cauchy_distribution(RealType a = 0.0, RealType b = 1.0);
Requires: 0 < b .
Effects: Constructs a cauchy_distribution object; a and b correspond to the respective parameters of the distribution.
Returns: The value of the a parameter with which the object was constructed.
Returns: The value of the b parameter with which the object was constructed.
26.5.8.5.5 Class template fisher_f_distribution [rand.dist.norm.f]
A fisher_f_distribution random number distribution
produces random numbers x≥0
distributed according to
the probability density function
![\[%
p(x\,|\,m,n)
= \frac{\Gamma\big((m+n)/2\big)}
{\Gamma(m/2) \; \Gamma(n/2)}
\cdot
\left(\frac{m}{n}\right)^{m/2}
\cdot
x^{(m/2)-1}
\cdot
{\left( 1 + \frac{m x}{n} \right)}^{-(m+n)/2}
\; \mbox{.}
\]](math/7429314193102074347.png)
template<class RealType = double>
class fisher_f_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructor and reset functions
explicit fisher_f_distribution(RealType m = 1, RealType n = 1);
explicit fisher_f_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
RealType m() const;
RealType n() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
explicit fisher_f_distribution(RealType m = 1, RealType n = 1);
Requires: 0 < m and 0 < n .
Effects: Constructs a fisher_f_distribution object; m and n correspond to the respective parameters of the distribution.
Returns: The value of the m parameter with which the object was constructed.
Returns: The value of the n parameter with which the object was constructed.
26.5.8.5.6 Class template student_t_distribution [rand.dist.norm.t]
A student_t_distribution random number distribution
produces random numbers x
distributed according to
the probability density function
![\[%
p(x\,|\,n)
= \frac{1}
{\sqrt{n \pi}}
\cdot \frac{\Gamma\big((n+1)/2\big)}
{\Gamma(n/2)}
\cdot \left( 1+\frac{x^2}{n} \right) ^ {-(n+1)/2}
\; \mbox{.}
\]](math/7766040669647665344.png)
template<class RealType = double>
class student_t_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructor and reset functions
explicit student_t_distribution(RealType n = 1);
explicit student_t_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
RealType n() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
Requires: 0 < n .
Effects: Constructs a student_t_distribution object; n corresponds to the parameter of the distribution.
Returns: The value of the n parameter with which the object was constructed.
26.5.8.6 Sampling distributions [rand.dist.samp]
26.5.8.6.1 Class template discrete_distribution [rand.dist.samp.discrete]
A discrete_distribution random number distribution produces random integers i, 0 ≤ i < n, distributed according to the discrete probability function P(i | p0,…,pn-1) = pi .
Unless specified otherwise, the distribution parameters are calculated as: pk = wk / S for k = 0, …, n-1 , in which the values wk, commonly known as the weights, shall be non-negative, non-NaN, and non-infinity. Moreover, the following relation shall hold: 0 < S = w0 + ⋯ + wn-1 .
template<class IntType = int>
class discrete_distribution{
public:
// types
typedef IntType result_type;
typedef unspecified param_type;
// constructor and reset functions
discrete_distribution();
template<class InputIterator>
discrete_distribution(InputIterator firstW, InputIterator lastW);
discrete_distribution(initializer_list<double> wl);
template<class UnaryOperation>
discrete_distribution(size_t nw, double xmin, double xmax, UnaryOperation fw);
explicit discrete_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
vector<double> probabilities() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
Effects: Constructs a discrete_distribution object with n = 1 and p0 = 1 . [ Note: Such an object will always deliver the value 0. — end note ]
template<class InputIterator>
discrete_distribution(InputIterator firstW, InputIterator lastW);
Requires: InputIterator shall satisfy the requirements of an input iterator (Table [tab:iterator.input.requirements]) type. Moreover, iterator_traits<InputIterator>::value_type shall denote a type that is convertible to double. If firstW == lastW, let n = 1 and w0 = 1 . Otherwise, [firstW, lastW) shall form a sequence w of length n > 0.
Effects: Constructs a discrete_distribution object with probabilities given by the formula above.
discrete_distribution(initializer_list<double> wl);
Effects: Same as discrete_distribution(wl.begin(), wl.end()).
template<class UnaryOperation>
discrete_distribution(size_t nw, double xmin, double xmax, UnaryOperation fw);
Requires: Each instance of type UnaryOperation shall be a function object ([function.objects]) whose return type shall be convertible to double. Moreover, double shall be convertible to the type of UnaryOperation's sole parameter. If nw = 0 , let n = 1 , otherwise let n = nw. The relation 0 < δ = (xmax - xmin) / n shall hold.
Effects: Constructs a discrete_distribution object with probabilities given by the formula above, using the following values: If nw = 0, let w0 = 1 . Otherwise, let wk = fw(xmin + k · δ + δ / 2) for k = 0, …, n-1 .
Complexity: The number of invocations of fw shall not exceed n.
vector<double> probabilities() const;
Returns: A vector<double> whose size member returns n and whose operator[] member returns pk when invoked with argument k for k = 0, …, n-1 .
26.5.8.6.2 Class template piecewise_constant_distribution [rand.dist.samp.pconst]
A piecewise_constant_distribution random number distribution produces random numbers x, b0 ≤ x < bn , uniformly distributed over each subinterval [ bi, bi+1 ) according to the probability density function p(x | b0,…,bn, ρ0,…,ρn-1) = ρi , for bi ≤ x < bi+1 .
The n+1 distribution parameters bi,
also known as this distribution's interval boundaries, shall satisfy the relation
bi < bi+1
for i = 0, …, n-1 .
Unless specified otherwise,
the remaining n distribution parameters are calculated as:
![\[%
\rho_k = \;
\frac{w_k}{S \cdot (b_{k+1}-b_k)}
\; \mbox{ for } k = 0, \ldots, n\!-\!1,
\]](math/3048641883406251400.png) in which the values wk,
commonly known as the weights, shall be non-negative, non-NaN, and non-infinity.
Moreover, the following relation shall hold:
0 < S = w0 + ⋯ + wn-1 .
in which the values wk,
commonly known as the weights, shall be non-negative, non-NaN, and non-infinity.
Moreover, the following relation shall hold:
0 < S = w0 + ⋯ + wn-1 .
template<class RealType = double>
class piecewise_constant_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructor and reset functions
piecewise_constant_distribution();
template<class InputIteratorB, class InputIteratorW>
piecewise_constant_distribution(InputIteratorB firstB, InputIteratorB lastB,
InputIteratorW firstW);
template<class UnaryOperation>
piecewise_constant_distribution(initializer_list<RealType> bl, UnaryOperation fw);
template<class UnaryOperation>
piecewise_constant_distribution(size_t nw, RealType xmin, RealType xmax, UnaryOperation fw);
explicit piecewise_constant_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
vector<result_type> intervals() const;
vector<result_type> densities() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
Effects: Constructs a piecewise_constant_distribution object with n = 1 , ρ0 = 1 , b0 = 0 , and b1 = 1 .
template<class InputIteratorB, class InputIteratorW>
piecewise_constant_distribution(InputIteratorB firstB, InputIteratorB lastB,
InputIteratorW firstW);
Requires: InputIteratorB and InputIteratorW shall each satisfy the requirements of an input iterator (Table [tab:iterator.input.requirements]) type. Moreover, iterator_traits<InputIteratorB>::value_type and iterator_traits<InputIteratorW>::value_type shall each denote a type that is convertible to double. If firstB == lastB or ++firstB == lastB, let n = 1 , w0 = 1 , b0 = 0 , and b1 = 1 . Otherwise, [firstB, lastB) shall form a sequence b of length n+1, the length of the sequence w starting from firstW shall be at least n, and any wk for k ≥ n shall be ignored by the distribution.
Effects: Constructs a piecewise_constant_distribution object with parameters as specified above.
template<class UnaryOperation>
piecewise_constant_distribution(initializer_list<RealType> bl, UnaryOperation fw);
Requires: Each instance of type UnaryOperation shall be a function object ([function.objects]) whose return type shall be convertible to double. Moreover, double shall be convertible to the type of UnaryOperation's sole parameter.
Effects: Constructs a piecewise_constant_distribution object with parameters taken or calculated from the following values: If bl.size() < 2, let n = 1, w0 = 1 , b0 = 0 , and b1 = 1 . Otherwise, let [bl.begin(), bl.end()) form a sequence b0, …, bn , and let wk = fw((bk+1 + bk) / 2) for k = 0, …, n-1 .
Complexity: The number of invocations of fw shall not exceed n.
template<class UnaryOperation>
piecewise_constant_distribution(size_t nw, RealType xmin, RealType xmax, UnaryOperation fw);
Requires: Each instance of type UnaryOperation shall be a function object ([function.objects]) whose return type shall be convertible to double. Moreover, double shall be convertible to the type of UnaryOperation's sole parameter. If nw = 0 , let n = 1 , otherwise let n = nw. The relation 0 < δ = (xmax - xmin) / n shall hold.
Effects: Constructs a piecewise_constant_distribution object with parameters taken or calculated from the following values: Let bk = xmin + k · δ for k = 0, …, n , and wk = fw(bk + δ / 2) for k = 0, …, n-1 .
Complexity: The number of invocations of fw shall not exceed n.
vector<result_type> intervals() const;
Returns: A vector<result_type> whose size member returns n + 1 and whose operator[] member returns bk when invoked with argument k for k = 0, …, n .
vector<result_type> densities() const;
Returns: A vector<result_type> whose size member returns n and whose operator[] member returns ρk when invoked with argument k for k = 0, …, n-1 .
26.5.8.6.3 Class template piecewise_linear_distribution [rand.dist.samp.plinear]
A piecewise_linear_distribution random number distribution
produces random numbers x,
b0 ≤ x < bn ,
distributed over each subinterval
[ bi, bi+1 )
according to the probability density function
![\[%
p(x\,|\,b_0,\ldots,b_n,\;\rho_0,\ldots,\rho_n)
= \rho_i \cdot {\frac{b_{i+1} - x}{b_{i+1} - b_i}}
+ \rho_{i+1} \cdot {\frac{x - b_i}{b_{i+1} - b_i}}
\; \mbox{,}
\mbox{ for } b_i \le x < b_{i+1}
\; \mbox{.}
\]](math/3323433200775997513.png)
The n+1 distribution parameters bi,
also known as this distribution's interval boundaries, shall satisfy the relation
bi < bi+1
for i = 0, …, n-1 .
Unless specified otherwise,
the remaining n+1 distribution parameters are calculated as
ρk = wk / S for k = 0, …, n ,
in which the values wk,
commonly known as the weights at boundaries, shall be non-negative, non-NaN, and non-infinity.
Moreover, the following relation shall hold:
![\[%
0 < S = \frac{1}{2}
\cdot \sum_{k=0}^{n-1} (w_k + w_{k+1}) \cdot (b_{k+1} - b_k)
\; \mbox{.}
\]](math/1746234017340765737.png)
template<class RealType = double>
class piecewise_linear_distribution{
public:
// types
typedef RealType result_type;
typedef unspecified param_type;
// constructor and reset functions
piecewise_linear_distribution();
template<class InputIteratorB, class InputIteratorW>
piecewise_linear_distribution(InputIteratorB firstB, InputIteratorB lastB,
InputIteratorW firstW);
template<class UnaryOperation>
piecewise_linear_distribution(initializer_list<RealType> bl, UnaryOperation fw);
template<class UnaryOperation>
piecewise_linear_distribution(size_t nw, RealType xmin, RealType xmax, UnaryOperation fw);
explicit piecewise_linear_distribution(const param_type& parm);
void reset();
// generating functions
template<class URNG>
result_type operator()(URNG& g);
template<class URNG>
result_type operator()(URNG& g, const param_type& parm);
// property functions
vector<result_type> intervals() const;
vector<result_type> densities() const;
param_type param() const;
void param(const param_type& parm);
result_type min() const;
result_type max() const;
};
Effects: Constructs a piecewise_linear_distribution object with n = 1 , ρ0 = ρ1 = 1 , b0 = 0 , and b1 = 1 .
template<class InputIteratorB, class InputIteratorW>
piecewise_linear_distribution(InputIteratorB firstB, InputIteratorB lastB,
InputIteratorW firstW);
Requires: InputIteratorB and InputIteratorW shall each satisfy the requirements of an input iterator (Table [tab:iterator.input.requirements]) type. Moreover, iterator_traits<InputIteratorB>::value_type and iterator_traits<InputIteratorW>::value_type shall each denote a type that is convertible to double. If firstB == lastB or ++firstB == lastB, let n = 1 , ρ0 = ρ1 = 1 , b0 = 0 , and b1 = 1 . Otherwise, [firstB, lastB) shall form a sequence b of length n+1, the length of the sequence w starting from firstW shall be at least n+1, and any wk for k ≥ n+1 shall be ignored by the distribution.
Effects: Constructs a piecewise_linear_distribution object with parameters as specified above.
template<class UnaryOperation>
piecewise_linear_distribution(initializer_list<RealType> bl, UnaryOperation fw);
Requires: Each instance of type UnaryOperation shall be a function object ([function.objects]) whose return type shall be convertible to double. Moreover, double shall be convertible to the type of UnaryOperation's sole parameter.
Effects: Constructs a piecewise_linear_distribution object with parameters taken or calculated from the following values: If bl.size() < 2, let n = 1, ρ0 = ρ1 = 1 , b0 = 0 , and b1 = 1 . Otherwise, let [bl.begin(), bl.end()) form a sequence b0, …, bn , and let wk = fw(bk) for k = 0, …, n .
Complexity: The number of invocations of fw shall not exceed n+1.
template<class UnaryOperation>
piecewise_linear_distribution(size_t nw, RealType xmin, RealType xmax, UnaryOperation fw);
Requires: Each instance of type UnaryOperation shall be a function object ([function.objects]) whose return type shall be convertible to double. Moreover, double shall be convertible to the type of UnaryOperation's sole parameter. If nw = 0 , let n = 1 , otherwise let n = nw. The relation 0 < δ = (xmax - xmin) / n shall hold.
Effects: Constructs a piecewise_linear_distribution object with parameters taken or calculated from the following values: Let bk = xmin + k · δ for k = 0, …, n , and wk = fw(bk) for k = 0, …, n .
Complexity: The number of invocations of fw shall not exceed n+1.
vector<result_type> intervals() const;
Returns: A vector<result_type> whose size member returns n + 1 and whose operator[] member returns bk when invoked with argument k for k = 0, …, n .
vector<result_type> densities() const;
Returns: A vector<result_type> whose size member returns n and whose operator[] member returns ρk when invoked with argument k for k = 0, …, n .
26.6 Numeric arrays [numarray]
26.6.1 Header <valarray> synopsis [valarray.syn]
#include <initializer_list>
namespace std {
template<class T> class valarray; // An array of type T
class slice; // a BLAS-like slice out of an array
template<class T> class slice_array;
class gslice; // a generalized slice out of an array
template<class T> class gslice_array;
template<class T> class mask_array; // a masked array
template<class T> class indirect_array; // an indirected array
template<class T> void swap(valarray<T>&, valarray<T>&) noexcept;
template<class T> valarray<T> operator* (const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator* (const valarray<T>&, const T&);
template<class T> valarray<T> operator* (const T&, const valarray<T>&);
template<class T> valarray<T> operator/ (const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator/ (const valarray<T>&, const T&);
template<class T> valarray<T> operator/ (const T&, const valarray<T>&);
template<class T> valarray<T> operator% (const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator% (const valarray<T>&, const T&);
template<class T> valarray<T> operator% (const T&, const valarray<T>&);
template<class T> valarray<T> operator+ (const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator+ (const valarray<T>&, const T&);
template<class T> valarray<T> operator+ (const T&, const valarray<T>&);
template<class T> valarray<T> operator- (const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator- (const valarray<T>&, const T&);
template<class T> valarray<T> operator- (const T&, const valarray<T>&);
template<class T> valarray<T> operator^ (const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator^ (const valarray<T>&, const T&);
template<class T> valarray<T> operator^ (const T&, const valarray<T>&);
template<class T> valarray<T> operator& (const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator& (const valarray<T>&, const T&);
template<class T> valarray<T> operator& (const T&, const valarray<T>&);
template<class T> valarray<T> operator| (const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator| (const valarray<T>&, const T&);
template<class T> valarray<T> operator| (const T&, const valarray<T>&);
template<class T> valarray<T> operator<<(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator<<(const valarray<T>&, const T&);
template<class T> valarray<T> operator<<(const T&, const valarray<T>&);
template<class T> valarray<T> operator>>(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator>>(const valarray<T>&, const T&);
template<class T> valarray<T> operator>>(const T&, const valarray<T>&);
template<class T> valarray<bool> operator&&(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator&&(const valarray<T>&, const T&);
template<class T> valarray<bool> operator&&(const T&, const valarray<T>&);
template<class T> valarray<bool> operator||(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator||(const valarray<T>&, const T&);
template<class T> valarray<bool> operator||(const T&, const valarray<T>&);
template<class T>
valarray<bool> operator==(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator==(const valarray<T>&, const T&);
template<class T> valarray<bool> operator==(const T&, const valarray<T>&);
template<class T>
valarray<bool> operator!=(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator!=(const valarray<T>&, const T&);
template<class T> valarray<bool> operator!=(const T&, const valarray<T>&);
template<class T>
valarray<bool> operator< (const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator< (const valarray<T>&, const T&);
template<class T> valarray<bool> operator< (const T&, const valarray<T>&);
template<class T>
valarray<bool> operator> (const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator> (const valarray<T>&, const T&);
template<class T> valarray<bool> operator> (const T&, const valarray<T>&);
template<class T>
valarray<bool> operator<=(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator<=(const valarray<T>&, const T&);
template<class T> valarray<bool> operator<=(const T&, const valarray<T>&);
template<class T>
valarray<bool> operator>=(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator>=(const valarray<T>&, const T&);
template<class T> valarray<bool> operator>=(const T&, const valarray<T>&);
template<class T> valarray<T> abs (const valarray<T>&);
template<class T> valarray<T> acos (const valarray<T>&);
template<class T> valarray<T> asin (const valarray<T>&);
template<class T> valarray<T> atan (const valarray<T>&);
template<class T> valarray<T> atan2(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> atan2(const valarray<T>&, const T&);
template<class T> valarray<T> atan2(const T&, const valarray<T>&);
template<class T> valarray<T> cos (const valarray<T>&);
template<class T> valarray<T> cosh (const valarray<T>&);
template<class T> valarray<T> exp (const valarray<T>&);
template<class T> valarray<T> log (const valarray<T>&);
template<class T> valarray<T> log10(const valarray<T>&);
template<class T> valarray<T> pow(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> pow(const valarray<T>&, const T&);
template<class T> valarray<T> pow(const T&, const valarray<T>&);
template<class T> valarray<T> sin (const valarray<T>&);
template<class T> valarray<T> sinh (const valarray<T>&);
template<class T> valarray<T> sqrt (const valarray<T>&);
template<class T> valarray<T> tan (const valarray<T>&);
template<class T> valarray<T> tanh (const valarray<T>&);
template <class T> unspecified1 begin(valarray<T>& v);
template <class T> unspecified2 begin(const valarray<T>& v);
template <class T> unspecified1 end(valarray<T>& v);
template <class T> unspecified2 end(const valarray<T>& v);
}
The header <valarray> defines five class templates (valarray, slice_array, gslice_array, mask_array, and indirect_array), two classes (slice and gslice), and a series of related function templates for representing and manipulating arrays of values.
The valarray array classes are defined to be free of certain forms of aliasing, thus allowing operations on these classes to be optimized.
Any function returning a valarray<T> is permitted to return an object of another type, provided all the const member functions of valarray<T> are also applicable to this type. This return type shall not add more than two levels of template nesting over the most deeply nested argument type.281
Implementations introducing such replacement types shall provide additional functions and operators as follows:
for every function taking a const valarray<T>& other than begin and end ([valarray.range]), identical functions taking the replacement types shall be added;
for every function taking two const valarray<T>& arguments, identical functions taking every combination of const valarray<T>& and replacement types shall be added.
In particular, an implementation shall allow a valarray<T> to be constructed from such replacement types and shall allow assignments and computed assignments of such types to valarray<T>, slice_array<T>, gslice_array<T>, mask_array<T> and indirect_array<T> objects.
These library functions are permitted to throw a bad_alloc ([bad.alloc]) exception if there are not sufficient resources available to carry out the operation. Note that the exception is not mandated.
26.6.2 Class template valarray [template.valarray]
26.6.2.1 Class template valarray overview [template.valarray.overview]
namespace std {
template<class T> class valarray {
public:
typedef T value_type;
// [valarray.cons] construct/destroy:
valarray();
explicit valarray(size_t);
valarray(const T&, size_t);
valarray(const T*, size_t);
valarray(const valarray&);
valarray(valarray&&) noexcept;
valarray(const slice_array<T>&);
valarray(const gslice_array<T>&);
valarray(const mask_array<T>&);
valarray(const indirect_array<T>&);
valarray(initializer_list<T>);
~valarray();
// [valarray.assign] assignment:
valarray<T>& operator=(const valarray<T>&);
valarray<T>& operator=(valarray<T>&&) noexcept;
valarray& operator=(initializer_list<T>);
valarray<T>& operator=(const T&);
valarray<T>& operator=(const slice_array<T>&);
valarray<T>& operator=(const gslice_array<T>&);
valarray<T>& operator=(const mask_array<T>&);
valarray<T>& operator=(const indirect_array<T>&);
// [valarray.access] element access:
const T& operator[](size_t) const;
T& operator[](size_t);
// [valarray.sub] subset operations:
valarray<T> operator[](slice) const;
slice_array<T> operator[](slice);
valarray<T> operator[](const gslice&) const;
gslice_array<T> operator[](const gslice&);
valarray<T> operator[](const valarray<bool>&) const;
mask_array<T> operator[](const valarray<bool>&);
valarray<T> operator[](const valarray<size_t>&) const;
indirect_array<T> operator[](const valarray<size_t>&);
// [valarray.unary] unary operators:
valarray<T> operator+() const;
valarray<T> operator-() const;
valarray<T> operator~() const;
valarray<bool> operator!() const;
// [valarray.cassign] computed assignment:
valarray<T>& operator*= (const T&);
valarray<T>& operator/= (const T&);
valarray<T>& operator%= (const T&);
valarray<T>& operator+= (const T&);
valarray<T>& operator-= (const T&);
valarray<T>& operator^= (const T&);
valarray<T>& operator&= (const T&);
valarray<T>& operator|= (const T&);
valarray<T>& operator<<=(const T&);
valarray<T>& operator>>=(const T&);
valarray<T>& operator*= (const valarray<T>&);
valarray<T>& operator/= (const valarray<T>&);
valarray<T>& operator%= (const valarray<T>&);
valarray<T>& operator+= (const valarray<T>&);
valarray<T>& operator-= (const valarray<T>&);
valarray<T>& operator^= (const valarray<T>&);
valarray<T>& operator|= (const valarray<T>&);
valarray<T>& operator&= (const valarray<T>&);
valarray<T>& operator<<=(const valarray<T>&);
valarray<T>& operator>>=(const valarray<T>&);
// [valarray.members] member functions:
void swap(valarray&) noexcept;
size_t size() const;
T sum() const;
T min() const;
T max() const;
valarray<T> shift (int) const;
valarray<T> cshift(int) const;
valarray<T> apply(T func(T)) const;
valarray<T> apply(T func(const T&)) const;
void resize(size_t sz, T c = T());
};
}
The class template valarray<T> is a one-dimensional smart array, with elements numbered sequentially from zero. It is a representation of the mathematical concept of an ordered set of values. The illusion of higher dimensionality may be produced by the familiar idiom of computed indices, together with the powerful subsetting capabilities provided by the generalized subscript operators.282
An implementation is permitted to qualify any of the functions declared in <valarray> as inline.
The intent is to specify an array template that has the minimum functionality necessary to address aliasing ambiguities and the proliferation of temporaries. Thus, the valarray template is neither a matrix class nor a field class. However, it is a very useful building block for designing such classes.
26.6.2.2 valarray constructors [valarray.cons]
The array created by this constructor has a length equal to the value of the argument. The elements of the array are value-initialized ([dcl.init]).
The array created by this constructor has a length equal to the second argument. The elements of the array are initialized with the value of the first argument.
The array created by this constructor has a length equal to the second argument n. The values of the elements of the array are initialized with the first n values pointed to by the first argument.285 If the value of the second argument is greater than the number of values pointed to by the first argument, the behavior is undefined.
The array created by this constructor has the same length as the argument array. The elements are initialized with the values of the corresponding elements of the argument array.286
valarray(valarray<T>&& v) noexcept;
The array created by this constructor has the same length as the argument array. The elements are initialized with the values of the corresponding elements of the argument array.
Complexity: Constant.
valarray(initializer_list<T> il);
Effects: Same as valarray(il.begin(), il.size()).
valarray(const slice_array<T>&);
valarray(const gslice_array<T>&);
valarray(const mask_array<T>&);
valarray(const indirect_array<T>&);
These conversion constructors convert one of the four reference templates to a valarray.
The destructor is applied to every element of *this; an implementation may return all allocated memory.
For convenience, such objects are referred to as “arrays” throughout the remainder of [numarray].
This default constructor is essential, since arrays of valarray may be useful. After initialization, the length of an empty array can be increased with the resize member function.
This constructor is the preferred method for converting a C array to a valarray object.
This copy constructor creates a distinct array rather than an alias. Implementations in which arrays share storage are permitted, but they shall implement a copy-on-reference mechanism to ensure that arrays are conceptually distinct.
26.6.2.3 valarray assignment [valarray.assign]
valarray<T>& operator=(const valarray<T>& v);
Each element of the *this array is assigned the value of the corresponding element of the argument array. If the length of v is not equal to the length of *this , resizes *this to make the two arrays the same length, as if by calling resize(v.size()), before performing the assignment.
Postcondition: size() == v.size().
valarray<T>& operator=(valarray<T>&& v) noexcept;
Effects: *this obtains the value of v. The value of v after the assignment is not specified.
Complexity: Linear.
valarray& operator=(initializer_list<T> il);
Effects: *this = valarray(il).
Returns: *this.
valarray<T>& operator=(const T&);
The scalar assignment operator causes each element of the *this array to be assigned the value of the argument.
valarray<T>& operator=(const slice_array<T>&);
valarray<T>& operator=(const gslice_array<T>&);
valarray<T>& operator=(const mask_array<T>&);
valarray<T>& operator=(const indirect_array<T>&);
Requires: The length of the array to which the argument refers equals size().
These operators allow the results of a generalized subscripting operation to be assigned directly to a valarray.
If the value of an element in the left-hand side of a valarray assignment operator depends on the value of another element in that left-hand side, the resulting behavior is undefined.
26.6.2.4 valarray element access [valarray.access]
const T& operator[](size_t) const;
T& operator[](size_t);
The subscript operator returns a reference to the corresponding element of the array.
Thus, the expression (a[i] = q, a[i]) == q evaluates as true for any non-constant valarray<T> a, any T q, and for any size_t i such that the value of i is less than the length of a.
The expression &a[i+j] == &a[i] + j evaluates as true for all size_t i and size_t j such that i+j is less than the length of the array a.
Likewise, the expression &a[i] != &b[j] evaluates as true for any two arrays a and b and for any size_t i and size_t j such that i is less than the length of a and j is less than the length of b. This property indicates an absence of aliasing and may be used to advantage by optimizing compilers.287
The reference returned by the subscript operator for an array shall be valid until the member function resize(size_t, T) ([valarray.members]) is called for that array or until the lifetime of that array ends, whichever happens first.
Compilers may take advantage of inlining, constant propagation, loop fusion, tracking of pointers obtained from operator new, and other techniques to generate efficient valarrays.
26.6.2.5 valarray subset operations [valarray.sub]
The member operator[] is overloaded to provide several ways to select sequences of elements from among those controlled by *this. Each of these operations returns a subset of the array. The const-qualified versions return this subset as a new valarray object. The non-const versions return a class template object which has reference semantics to the original array, working in conjunction with various overloads of operator= and other assigning operators to allow selective replacement (slicing) of the controlled sequence. In each case the selected element(s) must exist.
Returns: An object of class valarray<T> containing those elements of the controlled sequence designated by slicearr. [ Example:
const valarray<char> v0("abcdefghijklmnop", 16);
// v0[slice(2, 5, 3)] returns valarray<char>("cfilo", 5)
— end example ]
slice_array<T> operator[](slice slicearr);
Returns: An object that holds references to elements of the controlled sequence selected by slicearr. [ Example:
valarray<char> v0("abcdefghijklmnop", 16);
valarray<char> v1("ABCDE", 5);
v0[slice(2, 5, 3)] = v1;
// v0 == valarray<char>("abAdeBghCjkDmnEp", 16);
— end example ]
valarray<T> operator[](const gslice& gslicearr) const;
Returns: An object of class valarray<T> containing those elements of the controlled sequence designated by gslicearr. [ Example:
const valarray<char> v0("abcdefghijklmnop", 16);
const size_t lv[] = { 2, 3 };
const size_t dv[] = { 7, 2 };
const valarray<size_t> len(lv, 2), str(dv, 2);
// v0[gslice(3, len, str)] returns
// valarray<char>("dfhkmo", 6)
— end example ]
gslice_array<T> operator[](const gslice& gslicearr);
Returns: An object that holds references to elements of the controlled sequence selected by gslicearr. [ Example:
valarray<char> v0("abcdefghijklmnop", 16);
valarray<char> v1("ABCDE", 5);
const size_t lv[] = { 2, 3 };
const size_t dv[] = { 7, 2 };
const valarray<size_t> len(lv, 2), str(dv, 2);
v0[gslice(3, len, str)] = v1;
// v0 == valarray<char>("abcAeBgCijDlEnFp", 16)
— end example ]
valarray<T> operator[](const valarray<bool>& boolarr) const;
Returns: An object of class valarray<T> containing those elements of the controlled sequence designated by boolarr. [ Example:
const valarray<char> v0("abcdefghijklmnop", 16);
const bool vb[] = { false, false, true, true, false, true };
// v0[valarray<bool>(vb, 6)] returns
// valarray<char>("cdf", 3)
— end example ]
mask_array<T> operator[](const valarray<bool>& boolarr);
Returns: An object that holds references to elements of the controlled sequence selected by boolarr. [ Example:
valarray<char> v0("abcdefghijklmnop", 16);
valarray<char> v1("ABC", 3);
const bool vb[] = { false, false, true, true, false, true };
v0[valarray<bool>(vb, 6)] = v1;
// v0 == valarray<char>("abABeCghijklmnop", 16)
— end example ]
valarray<T> operator[](const valarray<size_t>& indarr) const;
Returns: An object of class valarray<T> containing those elements of the controlled sequence designated by indarr. [ Example:
const valarray<char> v0("abcdefghijklmnop", 16);
const size_t vi[] = { 7, 5, 2, 3, 8 };
// v0[valarray<size_t>(vi, 5)] returns
// valarray<char>("hfcdi", 5)
— end example ]
indirect_array<T> operator[](const valarray<size_t>& indarr);
Returns: An object that holds references to elements of the controlled sequence selected by indarr. [ Example:
valarray<char> v0("abcdefghijklmnop", 16);
valarray<char> v1("ABCDE", 5);
const size_t vi[] = { 7, 5, 2, 3, 8 };
v0[valarray<size_t>(vi, 5)] = v1;
// v0 == valarray<char>("abCDeBgAEjklmnop", 16)
— end example ]
26.6.2.6 valarray unary operators [valarray.unary]
valarray<T> operator+() const;
valarray<T> operator-() const;
valarray<T> operator~() const;
valarray<bool> operator!() const;
Each of these operators may only be instantiated for a type T to which the indicated operator can be applied and for which the indicated operator returns a value which is of type T (bool for operator!) or which may be unambiguously implicitly converted to type T (bool for operator!).
Each of these operators returns an array whose length is equal to the length of the array. Each element of the returned array is initialized with the result of applying the indicated operator to the corresponding element of the array.
26.6.2.7 valarray computed assignment [valarray.cassign]
valarray<T>& operator*= (const valarray<T>&);
valarray<T>& operator/= (const valarray<T>&);
valarray<T>& operator%= (const valarray<T>&);
valarray<T>& operator+= (const valarray<T>&);
valarray<T>& operator-= (const valarray<T>&);
valarray<T>& operator^= (const valarray<T>&);
valarray<T>& operator&= (const valarray<T>&);
valarray<T>& operator|= (const valarray<T>&);
valarray<T>& operator<<=(const valarray<T>&);
valarray<T>& operator>>=(const valarray<T>&);
Each of these operators may only be instantiated for a type T to which the indicated operator can be applied. Each of these operators performs the indicated operation on each of its elements and the corresponding element of the argument array.
The array is then returned by reference.
If the value of an element in the left-hand side of a valarray computed assignment operator depends on the value of another element in that left hand side, the resulting behavior is undefined.
valarray<T>& operator*= (const T&);
valarray<T>& operator/= (const T&);
valarray<T>& operator%= (const T&);
valarray<T>& operator+= (const T&);
valarray<T>& operator-= (const T&);
valarray<T>& operator^= (const T&);
valarray<T>& operator&= (const T&);
valarray<T>& operator|= (const T&);
valarray<T>& operator<<=(const T&);
valarray<T>& operator>>=(const T&);
Each of these operators may only be instantiated for a type T to which the indicated operator can be applied.
Each of these operators applies the indicated operation to each element of the array and the non-array argument.
The array is then returned by reference.
The appearance of an array on the left-hand side of a computed assignment does not invalidate references or pointers to the elements of the array.
26.6.2.8 valarray member functions [valarray.members]
void swap(valarray& v) noexcept;
Effects: *this obtains the value of v. v obtains the value of *this.
Complexity: Constant.
Returns: The number of elements in the array.
Complexity: Constant time.
This function may only be instantiated for a type T to which operator+= can be applied. This function returns the sum of all the elements of the array.
This function returns the minimum value contained in *this. The value returned for an array of length 0 is undefined. For an array of length 1, the value of element 0 is returned. For all other array lengths, the determination is made using operator<.
This function returns the maximum value contained in *this. The value returned for an array of length 0 is undefined. For an array of length 1, the value of element 0 is returned. For all other array lengths, the determination is made using operator<.
valarray<T> shift(int n) const;
This function returns an object of class valarray<T> of length size(), each of whose elements I is (*this)[I + n] if I + n is non-negative and less than size(), otherwise T(). Thus if element zero is taken as the leftmost element, a positive value of n shifts the elements left n places, with zero fill.
[ Example:
If the argument has the value -2,
the first two elements of the result will be value-initialized ([dcl.init]); the third element of the result will be assigned the value
of the first element of the argument; etc.
— end example ]
valarray<T> cshift(int n) const;
This function returns an object of class valarray<T> of length size() that is a circular shift of *this. If element zero is taken as the leftmost element, a non-negative value of n shifts the elements circularly left n places and a negative value of n shifts the elements circularly right -n places.
valarray<T> apply(T func(T)) const;
valarray<T> apply(T func(const T&)) const;
This member function changes the length of the *this array to sz and then assigns to each element the value of the second argument. Resizing invalidates all pointers and references to elements in the array.
26.6.3 valarray non-member operations [valarray.nonmembers]
26.6.3.1 valarray binary operators [valarray.binary]
template<class T> valarray<T> operator*
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator/
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator%
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator+
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator-
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator^
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator&
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator|
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator<<
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> operator>>
(const valarray<T>&, const valarray<T>&);
Each of these operators may only be instantiated for a type T to which the indicated operator can be applied and for which the indicated operator returns a value which is of type T or which can be unambiguously implicitly converted to type T.
Each of these operators returns an array whose length is equal to the lengths of the argument arrays. Each element of the returned array is initialized with the result of applying the indicated operator to the corresponding elements of the argument arrays.
template<class T> valarray<T> operator* (const valarray<T>&, const T&);
template<class T> valarray<T> operator* (const T&, const valarray<T>&);
template<class T> valarray<T> operator/ (const valarray<T>&, const T&);
template<class T> valarray<T> operator/ (const T&, const valarray<T>&);
template<class T> valarray<T> operator% (const valarray<T>&, const T&);
template<class T> valarray<T> operator% (const T&, const valarray<T>&);
template<class T> valarray<T> operator+ (const valarray<T>&, const T&);
template<class T> valarray<T> operator+ (const T&, const valarray<T>&);
template<class T> valarray<T> operator- (const valarray<T>&, const T&);
template<class T> valarray<T> operator- (const T&, const valarray<T>&);
template<class T> valarray<T> operator^ (const valarray<T>&, const T&);
template<class T> valarray<T> operator^ (const T&, const valarray<T>&);
template<class T> valarray<T> operator& (const valarray<T>&, const T&);
template<class T> valarray<T> operator& (const T&, const valarray<T>&);
template<class T> valarray<T> operator| (const valarray<T>&, const T&);
template<class T> valarray<T> operator| (const T&, const valarray<T>&);
template<class T> valarray<T> operator<<(const valarray<T>&, const T&);
template<class T> valarray<T> operator<<(const T&, const valarray<T>&);
template<class T> valarray<T> operator>>(const valarray<T>&, const T&);
template<class T> valarray<T> operator>>(const T&, const valarray<T>&);
Each of these operators may only be instantiated for a type T to which the indicated operator can be applied and for which the indicated operator returns a value which is of type T or which can be unambiguously implicitly converted to type T.
Each of these operators returns an array whose length is equal to the length of the array argument. Each element of the returned array is initialized with the result of applying the indicated operator to the corresponding element of the array argument and the non-array argument.
26.6.3.2 valarray logical operators [valarray.comparison]
template<class T> valarray<bool> operator==
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator!=
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator<
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator>
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator<=
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator>=
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator&&
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<bool> operator||
(const valarray<T>&, const valarray<T>&);
Each of these operators may only be instantiated for a type T to which the indicated operator can be applied and for which the indicated operator returns a value which is of type bool or which can be unambiguously implicitly converted to type bool.
Each of these operators returns a bool array whose length is equal to the length of the array arguments. Each element of the returned array is initialized with the result of applying the indicated operator to the corresponding elements of the argument arrays.
template<class T> valarray<bool> operator==(const valarray<T>&, const T&);
template<class T> valarray<bool> operator==(const T&, const valarray<T>&);
template<class T> valarray<bool> operator!=(const valarray<T>&, const T&);
template<class T> valarray<bool> operator!=(const T&, const valarray<T>&);
template<class T> valarray<bool> operator< (const valarray<T>&, const T&);
template<class T> valarray<bool> operator< (const T&, const valarray<T>&);
template<class T> valarray<bool> operator> (const valarray<T>&, const T&);
template<class T> valarray<bool> operator> (const T&, const valarray<T>&);
template<class T> valarray<bool> operator<=(const valarray<T>&, const T&);
template<class T> valarray<bool> operator<=(const T&, const valarray<T>&);
template<class T> valarray<bool> operator>=(const valarray<T>&, const T&);
template<class T> valarray<bool> operator>=(const T&, const valarray<T>&);
template<class T> valarray<bool> operator&&(const valarray<T>&, const T&);
template<class T> valarray<bool> operator&&(const T&, const valarray<T>&);
template<class T> valarray<bool> operator||(const valarray<T>&, const T&);
template<class T> valarray<bool> operator||(const T&, const valarray<T>&);
Each of these operators may only be instantiated for a type T to which the indicated operator can be applied and for which the indicated operator returns a value which is of type bool or which can be unambiguously implicitly converted to type bool.
Each of these operators returns a bool array whose length is equal to the length of the array argument. Each element of the returned array is initialized with the result of applying the indicated operator to the corresponding element of the array and the non-array argument.
26.6.3.3 valarray transcendentals [valarray.transcend]
template<class T> valarray<T> abs (const valarray<T>&);
template<class T> valarray<T> acos (const valarray<T>&);
template<class T> valarray<T> asin (const valarray<T>&);
template<class T> valarray<T> atan (const valarray<T>&);
template<class T> valarray<T> atan2
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> atan2(const valarray<T>&, const T&);
template<class T> valarray<T> atan2(const T&, const valarray<T>&);
template<class T> valarray<T> cos (const valarray<T>&);
template<class T> valarray<T> cosh (const valarray<T>&);
template<class T> valarray<T> exp (const valarray<T>&);
template<class T> valarray<T> log (const valarray<T>&);
template<class T> valarray<T> log10(const valarray<T>&);
template<class T> valarray<T> pow
(const valarray<T>&, const valarray<T>&);
template<class T> valarray<T> pow (const valarray<T>&, const T&);
template<class T> valarray<T> pow (const T&, const valarray<T>&);
template<class T> valarray<T> sin (const valarray<T>&);
template<class T> valarray<T> sinh (const valarray<T>&);
template<class T> valarray<T> sqrt (const valarray<T>&);
template<class T> valarray<T> tan (const valarray<T>&);
template<class T> valarray<T> tanh (const valarray<T>&);
Each of these functions may only be instantiated for a type T to which a unique function with the indicated name can be applied (unqualified). This function shall return a value which is of type T or which can be unambiguously implicitly converted to type T.
26.6.3.4 valarray specialized algorithms [valarray.special]
template <class T> void swap(valarray<T>& x, valarray<T>& y) noexcept;
Effects: x.swap(y).
26.6.4 Class slice [class.slice]
26.6.4.1 Class slice overview [class.slice.overview]
namespace std {
class slice {
public:
slice();
slice(size_t, size_t, size_t);
size_t start() const;
size_t size() const;
size_t stride() const;
};
}
The slice class represents a BLAS-like slice from an array. Such a slice is specified by a starting index, a length, and a stride.288
BLAS stands for Basic Linear Algebra Subprograms. C++ programs may instantiate this class. See, for example, Dongarra, Du Croz, Duff, and Hammerling: A set of Level 3 Basic Linear Algebra Subprograms; Technical Report MCS-P1-0888, Argonne National Laboratory (USA), Mathematics and Computer Science Division, August, 1988.
26.6.4.2 slice constructors [cons.slice]
slice();
slice(size_t start, size_t length, size_t stride);
slice(const slice&);
The default constructor is equivalent to slice(0, 0, 0). A default constructor is provided only to permit the declaration of arrays of slices. The constructor with arguments for a slice takes a start, length, and stride parameter.
[ Example: slice(3, 8, 2) constructs a slice which selects elements 3, 5, 7, ... 17 from an array. — end example ]
26.6.4.3 slice access functions [slice.access]
size_t start() const;
size_t size() const;
size_t stride() const;
Returns: The start, length, or stride specified by a slice object.
Complexity: Constant time.
26.6.5 Class template slice_array [template.slice.array]
26.6.5.1 Class template slice_array overview [template.slice.array.overview]
namespace std {
template <class T> class slice_array {
public:
typedef T value_type;
void operator= (const valarray<T>&) const;
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator^= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
slice_array(const slice_array&);
~slice_array();
const slice_array& operator=(const slice_array&) const;
void operator=(const T&) const;
slice_array() = delete; // as implied by declaring copy constructor above
};
}
The slice_array template is a helper template used by the slice subscript operator
slice_array<T> valarray<T>::operator[](slice);
It has reference semantics to a subset of an array specified by a slice object.
[ Example: The expression a[slice(1, 5, 3)] = b; has the effect of assigning the elements of b to a slice of the elements in a. For the slice shown, the elements selected from a are 1, 4, ..., 13. — end example ]
26.6.5.2 slice_array assignment [slice.arr.assign]
void operator=(const valarray<T>&) const;
const slice_array& operator=(const slice_array&) const;
These assignment operators have reference semantics, assigning the values of the argument array elements to selected elements of the valarray<T> object to which the slice_array object refers.
26.6.5.3 slice_array computed assignment [slice.arr.comp.assign]
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator^= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
These computed assignments have reference semantics, applying the indicated operation to the elements of the argument array and selected elements of the valarray<T> object to which the slice_array object refers.
26.6.5.4 slice_array fill function [slice.arr.fill]
void operator=(const T&) const;
This function has reference semantics, assigning the value of its argument to the elements of the valarray<T> object to which the slice_array object refers.
26.6.6 The gslice class [class.gslice]
26.6.6.1 The gslice class overview [class.gslice.overview]
namespace std {
class gslice {
public:
gslice();
gslice(size_t s, const valarray<size_t>& l, const valarray<size_t>& d);
size_t start() const;
valarray<size_t> size() const;
valarray<size_t> stride() const;
};
}
This class represents a generalized slice out of an array. A gslice is defined by a starting offset (s), a set of lengths (lj), and a set of strides (dj). The number of lengths shall equal the number of strides.
A
gslice
represents a mapping from a set of indices (ij),
equal in number to the number of strides, to a single index k.
It is useful for building multidimensional array classes using
the
valarray
template, which is one-dimensional.
The set of one-dimensional index values specified by a
gslice
are 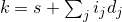 where the multidimensional indices ij range in value from
0 to lij - 1.
where the multidimensional indices ij range in value from
0 to lij - 1.
[ Example: The gslice specification
start = 3
length = {2, 4, 3}
stride = {19, 4, 1}
yields the sequence of one-dimensional indices
k = 3 + (0,1) × 19 + (0,1,2,3) × 4 + (0,1,2) × 1
which are ordered as shown in the following table:
(i0, i1, i2, k) = (0, 0, 0, 3), (0, 0, 1, 4), (0, 0, 2, 5), (0, 1, 0, 7), (0, 1, 1, 8), (0, 1, 2, 9), (0, 2, 0, 11), (0, 2, 1, 12), (0, 2, 2, 13), (0, 3, 0, 15), (0, 3, 1, 16), (0, 3, 2, 17), (1, 0, 0, 22), (1, 0, 1, 23), … (1, 3, 2, 36)
That is, the highest-ordered index turns fastest. — end example ]
It is possible to have degenerate generalized slices in which an address is repeated.
[ Example: If the stride parameters in the previous example are changed to {1, 1, 1}, the first few elements of the resulting sequence of indices will be
(0, 0, 0, 3), (0, 0, 1, 4), (0, 0, 2, 5), (0, 1, 0, 4), (0, 1, 1, 5), (0, 1, 2, 6), …
— end example ]
26.6.6.2 gslice constructors [gslice.cons]
gslice();
gslice(size_t start, const valarray<size_t>& lengths,
const valarray<size_t>& strides);
gslice(const gslice&);
The default constructor is equivalent to gslice(0, valarray<size_t>(), valarray<size_t>()). The constructor with arguments builds a gslice based on a specification of start, lengths, and strides, as explained in the previous section.
26.6.6.3 gslice access functions [gslice.access]
size_t start() const;
valarray<size_t> size() const;
valarray<size_t> stride() const;
Returns: The representation of the start, lengths, or strides specified for the gslice.
Complexity: start() is constant time. size() and stride() are linear in the number of strides.
26.6.7 Class template gslice_array [template.gslice.array]
26.6.7.1 Class template gslice_array overview [template.gslice.array.overview]
namespace std {
template <class T> class gslice_array {
public:
typedef T value_type;
void operator= (const valarray<T>&) const;
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator^= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
gslice_array(const gslice_array&);
~gslice_array();
const gslice_array& operator=(const gslice_array&) const;
void operator=(const T&) const;
gslice_array() = delete; // as implied by declaring copy constructor above
};
}
This template is a helper template used by the slice subscript operator
It has reference semantics to a subset of an array specified by a gslice object.
Thus, the expression a[gslice(1, length, stride)] = b has the effect of assigning the elements of b to a generalized slice of the elements in a.
26.6.7.2 gslice_array assignment [gslice.array.assign]
void operator=(const valarray<T>&) const;
const gslice_array& operator=(const gslice_array&) const;
These assignment operators have reference semantics, assigning the values of the argument array elements to selected elements of the valarray<T> object to which the gslice_array refers.
26.6.7.3 gslice_array [gslice.array.comp.assign]
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator^= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
These computed assignments have reference semantics, applying the indicated operation to the elements of the argument array and selected elements of the valarray<T> object to which the gslice_array object refers.
26.6.7.4 gslice_array fill function [gslice.array.fill]
void operator=(const T&) const;
This function has reference semantics, assigning the value of its argument to the elements of the valarray<T> object to which the gslice_array object refers.
26.6.8 Class template mask_array [template.mask.array]
26.6.8.1 Class template mask_array overview [template.mask.array.overview]
namespace std {
template <class T> class mask_array {
public:
typedef T value_type;
void operator= (const valarray<T>&) const;
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator^= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
mask_array(const mask_array&);
~mask_array();
const mask_array& operator=(const mask_array&) const;
void operator=(const T&) const;
mask_array() = delete; // as implied by declaring copy constructor above
};
}
This template is a helper template used by the mask subscript operator:
mask_array<T> valarray<T>::operator[](const valarray<bool>&).
It has reference semantics to a subset of an array specified by a boolean mask. Thus, the expression a[mask] = b; has the effect of assigning the elements of b to the masked elements in a (those for which the corresponding element in mask is true.)
26.6.8.2 mask_array assignment [mask.array.assign]
void operator=(const valarray<T>&) const;
const mask_array& operator=(const mask_array&) const;
These assignment operators have reference semantics, assigning the values of the argument array elements to selected elements of the valarray<T> object to which it refers.
26.6.8.3 mask_array computed assignment [mask.array.comp.assign]
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator^= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
These computed assignments have reference semantics, applying the indicated operation to the elements of the argument array and selected elements of the valarray<T> object to which the mask object refers.
26.6.8.4 mask_array fill function [mask.array.fill]
void operator=(const T&) const;
This function has reference semantics, assigning the value of its argument to the elements of the valarray<T> object to which the mask_array object refers.
26.6.9 Class template indirect_array [template.indirect.array]
26.6.9.1 Class template indirect_array overview [template.indirect.array.overview]
namespace std {
template <class T> class indirect_array {
public:
typedef T value_type;
void operator= (const valarray<T>&) const;
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator^= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
indirect_array(const indirect_array&);
~indirect_array();
const indirect_array& operator=(const indirect_array&) const;
void operator=(const T&) const;
indirect_array() = delete; // as implied by declaring copy constructor above
};
}
This template is a helper template used by the indirect subscript operator
indirect_array<T> valarray<T>::operator[](const valarray<size_t>&).
It has reference semantics to a subset of an array specified by an indirect_array. Thus the expression a[indirect] = b; has the effect of assigning the elements of b to the elements in a whose indices appear in indirect.
26.6.9.2 indirect_array assignment [indirect.array.assign]
void operator=(const valarray<T>&) const;
const indirect_array& operator=(const indirect_array&) const;
These assignment operators have reference semantics, assigning the values of the argument array elements to selected elements of the valarray<T> object to which it refers.
[ Example:
int addr[] = {2, 3, 1, 4, 4};
valarray<size_t> indirect(addr, 5);
valarray<double> a(0., 10), b(1., 5);
a[indirect] = b;
results in undefined behavior since element 4 is specified twice in the indirection. — end example ]
26.6.9.3 indirect_array computed assignment [indirect.array.comp.assign]
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator^= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
These computed assignments have reference semantics, applying the indicated operation to the elements of the argument array and selected elements of the valarray<T> object to which the indirect_array object refers.
26.6.9.4 indirect_array fill function [indirect.array.fill]
void operator=(const T&) const;
This function has reference semantics, assigning the value of its argument to the elements of the valarray<T> object to which the indirect_array object refers.
26.6.10 valarray range access [valarray.range]
In the begin and end function templates that follow, unspecified1 is a type that meets the requirements of a mutable random access iterator ([random.access.iterators]) whose value_type is the template parameter T and whose reference type is T&. unspecified2 is a type that meets the requirements of a constant random access iterator ([random.access.iterators]) whose value_type is the template parameter T and whose reference type is const T&.
The iterators returned by begin and end for an array are guaranteed to be valid until the member function resize(size_t, T) ([valarray.members]) is called for that array or until the lifetime of that array ends, whichever happens first.
template <class T> unspecified1 begin(valarray<T>& v);
template <class T> unspecified2 begin(const valarray<T>& v);
Returns: An iterator referencing the first value in the numeric array.
template <class T> unspecified1 end(valarray<T>& v);
template <class T> unspecified2 end(const valarray<T>& v);
Returns: An iterator referencing one past the last value in the numeric array.
26.7 Generalized numeric operations [numeric.ops]
26.7.1 Header <numeric> synopsis [numeric.ops.overview]
namespace std {
template <class InputIterator, class T>
T accumulate(InputIterator first, InputIterator last, T init);
template <class InputIterator, class T, class BinaryOperation>
T accumulate(InputIterator first, InputIterator last, T init,
BinaryOperation binary_op);
template <class InputIterator1, class InputIterator2, class T>
T inner_product(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, T init);
template <class InputIterator1, class InputIterator2, class T,
class BinaryOperation1, class BinaryOperation2>
T inner_product(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, T init,
BinaryOperation1 binary_op1,
BinaryOperation2 binary_op2);
template <class InputIterator, class OutputIterator>
OutputIterator partial_sum(InputIterator first,
InputIterator last,
OutputIterator result);
template <class InputIterator, class OutputIterator,
class BinaryOperation>
OutputIterator partial_sum(InputIterator first,
InputIterator last,
OutputIterator result,
BinaryOperation binary_op);
template <class InputIterator, class OutputIterator>
OutputIterator adjacent_difference(InputIterator first,
InputIterator last,
OutputIterator result);
template <class InputIterator, class OutputIterator,
class BinaryOperation>
OutputIterator adjacent_difference(InputIterator first,
InputIterator last,
OutputIterator result,
BinaryOperation binary_op);
template <class ForwardIterator, class T>
void iota(ForwardIterator first, ForwardIterator last, T value);
}
The requirements on the types of algorithms' arguments that are described in the introduction to Clause [algorithms] also apply to the following algorithms.
26.7.2 Accumulate [accumulate]
template <class InputIterator, class T>
T accumulate(InputIterator first, InputIterator last, T init);
template <class InputIterator, class T, class BinaryOperation>
T accumulate(InputIterator first, InputIterator last, T init,
BinaryOperation binary_op);
Effects: Computes its result by initializing the accumulator acc with the initial value init and then modifies it with acc = acc + *i or acc = binary_op(acc, *i) for every iterator i in the range [first,last) in order.289
Requires: T shall meet the requirements of CopyConstructible (Table [copyconstructible]) and CopyAssignable (Table [copyassignable]) types. In the range [first,last], binary_op shall neither modify elements nor invalidate iterators or subranges.290
accumulate is similar to the APL reduction operator and Common Lisp reduce function, but it avoids the difficulty of defining the result of reduction on an empty sequence by always requiring an initial value.
The use of fully closed ranges is intentional
26.7.3 Inner product [inner.product]
template <class InputIterator1, class InputIterator2, class T>
T inner_product(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, T init);
template <class InputIterator1, class InputIterator2, class T,
class BinaryOperation1, class BinaryOperation2>
T inner_product(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, T init,
BinaryOperation1 binary_op1,
BinaryOperation2 binary_op2);
Effects: Computes its result by initializing the accumulator acc with the initial value init and then modifying it with acc = acc + (*i1) * (*i2) or acc = binary_op1(acc, binary_op2(*i1, *i2)) for every iterator i1 in the range [first1,last1) and iterator i2 in the range [first2,first2 + (last1 - first1)) in order.
Requires: T shall meet the requirements of CopyConstructible (Table [copyconstructible]) and CopyAssignable (Table [copyassignable]) types. In the ranges [first1,last1] and [first2,first2 + (last1 - first1)] binary_op1 and binary_op2 shall neither modify elements nor invalidate iterators or subranges.291
The use of fully closed ranges is intentional
26.7.4 Partial sum [partial.sum]
template <class InputIterator, class OutputIterator>
OutputIterator partial_sum(
InputIterator first, InputIterator last,
OutputIterator result);
template
<class InputIterator, class OutputIterator, class BinaryOperation>
OutputIterator partial_sum(
InputIterator first, InputIterator last,
OutputIterator result, BinaryOperation binary_op);
Effects: For a non-empty range, the function creates an accumulator acc whose type is InputIterator's value type, initializes it with *first, and assigns the result to *result. For every iterator i in [first + 1,last) in order, acc is then modified by acc = acc + *i or acc = binary_op(acc, *i) and the result is assigned to *(result + (i - first)).
Returns: result + (last - first).
Complexity: Exactly (last - first) - 1 applications of the binary operation.
Requires: InputIterator's value type shall be constructible from the type of *first. The result of the expression acc + *i or binary_op(acc, *i) shall be implicitly convertible to InputIterator's value type. acc shall be writable to the result output iterator. In the ranges [first,last] and [result,result + (last - first)] binary_op shall neither modify elements nor invalidate iterators or subranges.292
Remarks: result may be equal to first.
The use of fully closed ranges is intentional.
26.7.5 Adjacent difference [adjacent.difference]
template <class InputIterator, class OutputIterator>
OutputIterator adjacent_difference(
InputIterator first, InputIterator last,
OutputIterator result);
template <class InputIterator, class OutputIterator, class BinaryOperation>
OutputIterator adjacent_difference(
InputIterator first, InputIterator last,
OutputIterator result,
BinaryOperation binary_op);
Effects: For a non-empty range, the function creates an accumulator acc whose type is InputIterator's value type, initializes it with *first, and assigns the result to *result. For every iterator i in [first + 1,last) in order, creates an object val whose type is InputIterator's value type, initializes it with *i, computes val - acc or binary_op(val, acc), assigns the result to *(result + (i - first)), and move assigns from val to acc.
Requires: InputIterator's value type shall be MoveAssignable (Table [moveassignable]) and shall be constructible from the type of *first. acc shall be writable to the result output iterator. The result of the expression val - acc or binary_op(val, acc) shall be writable to the result output iterator. In the ranges [first,last] and [result,result + (last - first)], binary_op shall neither modify elements nor invalidate iterators or subranges.293
Remarks: result may be equal to first.
Returns: result + (last - first).
Complexity: Exactly (last - first) - 1 applications of the binary operation.
The use of fully closed ranges is intentional.
26.7.6 Iota [numeric.iota]
template <class ForwardIterator, class T>
void iota(ForwardIterator first, ForwardIterator last, T value);
Requires: T shall be convertible to ForwardIterator's value type. The expression ++val, where val has type T, shall be well formed.
Effects: For each element referred to by the iterator i in the range [first,last), assigns *i = value and increments value as if by ++value.
Complexity: Exactly last - first increments and assignments.
26.8 C library [c.math]
[ Note: The overloads provided in C by type-generic macros are already provided in <ccomplex> and <cmath> by “sufficient” additional overloads. — end note ]
Tables [tab:numerics.hdr.cmath] and [tab:numerics.hdr.cstdlib] describe headers <cmath> and <cstdlib>, respectively.
| Type | Name(s) | |||
| Macros: | ||||
| FP_FAST_FMA | FP_ILOGBNAN | FP_SUBNORMAL | HUGE_VALL | MATH_ERRNO |
| FP_FAST_FMAF | FP_INFINITE | FP_ZERO | INFINITY | MATH_ERREXCEPT |
| FP_FAST_FMAL | FP_NAN | HUGE_VAL | NAN | math_errhandling |
| FP_ILOGB0 | FP_NORMAL | HUGE_VALF | ||
| Types: | double_t | float_t | ||
| Math Functions: | ||||
| abs | cosh | fmod | logb | remquo |
| acos | erf | frexp | lrint | rint |
| acosh | erfc | hypot | lround | round |
| asin | exp2 | ilogb | modf | scalbln |
| asinh | exp | ldexp | nan | scalbn |
| atan | expm1 | lgamma | nanf | sin |
| atan2 | fabs | llrint | nanl | sinh |
| atanh | fdim | llround | nearbyint | sqrt |
| cbrt | floor | log | nextafter | tan |
| ceil | fma | log10 | nexttoward | tanh |
| copysign | fmax | log1p | pow | tgamma |
| cos | fmin | log2 | remainder | trunc |
| Classification/comparison Functions: | ||||
| fpclassify | isgreaterequal | islessequal | isnan | isunordered |
| isfinite | isinf | islessgreater | isnormal | signbit |
| isgreater | isless | |||
| Type | Name(s) | |
| Macro: | RAND_MAX | |
| Types: | ||
| div_t | ldiv_t | lldiv_t |
| Functions: | ||
| abs | ldiv | rand |
| div | llabs | srand |
| labs | lldiv | |
The contents of these headers are the same as the Standard C library headers <math.h> and <stdlib.h> respectively, with the following changes:
The rand function has the semantics specified in the C standard, except that the implementation may specify that particular library functions may call rand. It is implementation-defined whether the rand function may introduce data races ([res.on.data.races]). [ Note: The random number generation ([rand]) facilities in this standard are often preferable to rand, because rand's underlying algorithm is unspecified. Use of rand therefore continues to be nonportable, with unpredictable and oft-questionable quality and performance. — end note ]
In addition to the int versions of certain math functions in <cstdlib>, C++ adds long and long long overloaded versions of these functions, with the same semantics.
long abs(long); // labs() long long abs(long long); // llabs() ldiv_t div(long, long); // ldiv() lldiv_t div(long long, long long); // lldiv()
In addition to the double versions of the math functions in <cmath>, C++ adds float and long double overloaded versions of these functions, with the same semantics.
The added signatures are:
float abs(float);
float acos(float);
float acosh(float);
float asin(float);
float asinh(float);
float atan(float);
float atan2(float, float);
float atanh(float);
float cbrt(float);
float ceil(float);
float copysign(float, float);
float cos(float);
float cosh(float);
float erf(float);
float erfc(float);
float exp(float);
float exp2(float);
float expm1(float);
float fabs(float);
float fdim(float, float);
float floor(float);
float fma(float, float, float);
float fmax(float, float);
float fmin(float, float);
float fmod(float, float);
float frexp(float, int*);
float hypot(float, float);
int ilogb(float);
float ldexp(float, int);
float lgamma(float);
long long llrint(float);
long long llround(float);
float log(float);
float log10(float);
float log1p(float);
float log2(float);
float logb(float);
long lrint(float);
long lround(float);
float modf(float, float*);
float nearbyint(float);
float nextafter(float, float);
float nexttoward(float, long double);
float pow(float, float);
float remainder(float, float);
float remquo(float, float, int *);
float rint(float);
float round(float);
float scalbln(float, long);
float scalbn(float, int);
float sin(float);
float sinh(float);
float sqrt(float);
float tan(float);
float tanh(float);
float tgamma(float);
float trunc(float);
double abs(double); // fabs()
long double abs(long double);
long double acos(long double);
long double acosh(long double);
long double asin(long double);
long double asinh(long double);
long double atan(long double);
long double atan2(long double, long double);
long double atanh(long double);
long double cbrt(long double);
long double ceil(long double);
long double copysign(long double, long double);
long double cos(long double);
long double cosh(long double);
long double erf(long double);
long double erfc(long double);
long double exp(long double);
long double exp2(long double);
long double expm1(long double);
long double fabs(long double);
long double fdim(long double, long double);
long double floor(long double);
long double fma(long double, long double, long double);
long double fmax(long double, long double);
long double fmin(long double, long double);
long double fmod(long double, long double);
long double frexp(long double, int*);
long double hypot(long double, long double);
int ilogb(long double);
long double ldexp(long double, int);
long double lgamma(long double);
long long llrint(long double);
long long llround(long double);
long double log(long double);
long double log10(long double);
long double log1p(long double);
long double log2(long double);
long double logb(long double);
long lrint(long double);
long lround(long double);
long double modf(long double, long double*);
long double nearbyint(long double);
long double nextafter(long double, long double);
long double nexttoward(long double, long double);
long double pow(long double, long double);
long double remainder(long double, long double);
long double remquo(long double, long double, int *);
long double rint(long double);
long double round(long double);
long double scalbln(long double, long);
long double scalbn(long double, int);
long double sin(long double);
long double sinh(long double);
long double sqrt(long double);
long double tan(long double);
long double tanh(long double);
long double tgamma(long double);
long double trunc(long double);
The classification/comparison functions behave the same as the C macros with the corresponding names defined in 7.12.3, Classification macros, and 7.12.14, Comparison macros in the C Standard. Each function is overloaded for the three floating-point types, as follows:
int fpclassify(float x); bool isfinite(float x); bool isinf(float x); bool isnan(float x); bool isnormal(float x); bool signbit(float x); bool isgreater(float x, float y); bool isgreaterequal(float x, float y); bool isless(float x, float y); bool islessequal(float x, float y); bool islessgreater(float x, float y); bool isunordered(float x, float y); int fpclassify(double x); bool isfinite(double x); bool isinf(double x); bool isnan(double x); bool isnormal(double x); bool signbit(double x); bool isgreater(double x, double y); bool isgreaterequal(double x, double y); bool isless(double x, double y); bool islessequal(double x, double y); bool islessgreater(double x, double y); bool isunordered(double x, double y); int fpclassify(long double x); bool isfinite(long double x); bool isinf(long double x); bool isnan(long double x); bool isnormal(long double x); bool signbit(long double x); bool isgreater(long double x, long double y); bool isgreaterequal(long double x, long double y); bool isless(long double x, long double y); bool islessequal(long double x, long double y); bool islessgreater(long double x, long double y); bool isunordered(long double x, long double y);
Moreover, there shall be additional overloads sufficient to ensure:
If any arithmetic argument corresponding to a double parameter has type long double, then all arithmetic arguments corresponding to double parameters are effectively cast to long double.
Otherwise, if any arithmetic argument corresponding to a double parameter has type double or an integer type, then all arithmetic arguments corresponding to double parameters are effectively cast to double.
Otherwise, all arithmetic arguments corresponding to double parameters have type float.
See also: ISO C 7.5, 7.10.2, 7.10.6.